Раз наш участок можно будет огородить забором в 300 метров, то его периметр не должен превышать 300.
Пусть 
и 
- две стороны нашего участка, тогда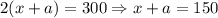 
.
Площадь прямоугольника - произведение двух смежных его сторон.
Составим функцию площади нашего участка в зависимости, например, от стороны .
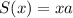
Но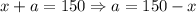 
, следовательно, наша функция принимает вид
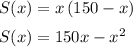
С производной найдём экстремум данной функции.
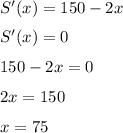
Т.к. исходная функция - парабола с опущенными вниз ветвями, то данная точка - максимум функции. Следовательно, при условии периметра в 300 метров, для достижения наибольшей площади участка одна из сторон должна быть равна 75 метров, значит, другая сторона также должна быть 75 метров (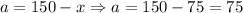
).
Получаем максимальную площадь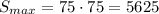 
квадратных метров.
ответ.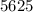 
кв. м.
При x>0 функция в левой части возрастает, а функция в правой части убывает, значит их графики пересекаются лишь в одной точке, ясно что эта точка - x=25. При этом очевидно, что всюду ЛЕВЕЕ этой точки график функции 27-x лежит выше графика функции логарифма на координантной плоскости. Ну ясно же, один график шел снизу вверх (логарифм), а другой сверху вниз (27-x), в этой точке они пересеклись и для x>25 уже наоборот график логарифма будет лежать выше.
Поэтому ответ: 0<x≤25
"Расписать подробно":
Функция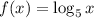 
определена при x>0 и монотонно возрастает, так как основание логарифма больше 1.
Функция g(x)=27-x убывает, так как (27-x)'=-1
x=25 - корень уравнения f(x)=g(x). Причем корень единственный, это следует из выше написанного.
Тогда очевидно, что f(x)≤g(x) при 0<x≤25
P.S.
Функции тут простые, поэтому можно вообще забить на аналитическое решение и его обоснование, а решить графически. Начертить графики и на чертеже сразу будет видно то, что аналитически приходится доказывать с свойств функций.
D=16
X1= 6+4/2
X1=5
X2= 6-4/2
X2=1