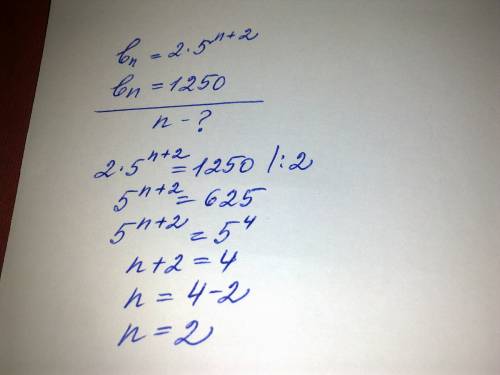
целые решения уравнения это делители свободного члена.
Можно подставлять все делители свободного члена, но нам нужно только 2, если уравнение 4 степение, и 3 если уравнение 5 степени(так как в этом случае мы разложим ее в таком виде (x-x1)(x-x2)(ax^2+bx+c)=0, а такое уравнение решить легко).
в первом это числа -2 и 3.
получаем x^4-x^3-5x^2-x-6=(x-3)(x+2)(x^2+1). теперь нужно каждый множитель приравнять нулю решить уравнения а потом обьеденить все корни:
x-3=0 => x=3; x+2=0 => x=-2; x^2+1=0 нет корней. ответ: -2; 3
а другие уравнения напиши в другой теме. по правилам сайта
Пользователи признают, что задания, которые содержат большое количество задач, требующих решения, должны быть разделены на два или несколько заданий и в таком виде добавлены в Сервис для других Пользователей. То есть в одном задании не может быть несколько задач.
условие безобразно оформлено, пришлось как-то догадываться, что имелось ввиду, так что, если я решил не те примеры, что вы ждали - ваша вина, надо понятно оформлять.
Это устные упражнения на тему (a^3 + b^3)/(a^2 - a*b + b^2) = (a + b); (ну, конечно, и сумма и разность кубов сюда укладываются, для отрицательных чисел целые степени определены.)
в случае А) a = 1/2000 b = - 1/1999 (ну, в смысле число в минус первой степени);
ответ 1/2000 - 1/1999 = - 1/(1999*2000) = - 1/3998000;
Б) a = 1/1222 b = 1/777,
ответ 1/1222 + 1/777 = 1999/949494; может это и можно сократить, но ...