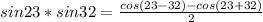
x² + (m - 1)x + m² - 1,5 = 0
По теореме Виета :
x₁ + x₂ = - (m - 1)
x₁ * x₂ = m² - 1,5
x₁² + x₂² = (x₁ + x₂)² - 2x₁ * x₂ = (- (m - 1))² - 2 * (m² - 1,5) = m² - 2m + 1 - 2m² + 3 = - m² - 2m + 4
Найдём производную полученного выражения :
(- m² - 2m + 4)'= -2m - 2
Приравняем к нулю и найдём нули производной :
- 2m - 2 = 0
m + 1 = 0
m = - 1
Отметим полученное число на числовой прямой и найдём знаки производной на промежутках, на которые разбивается числовая прямая :
+ -
- 1
↑ max ↓
ответ : при m = - 1 сумма корней уравнения наибольшая
Нужно использовать следующие свойства числовых неравенств:
1. К обеим частям верного числового неравенства можно прибавить одно и то же число и получится верное числовое неравенство, т.е.:
если а < b и с - любое число, то a + c < b + c.
2. Обе части верного числового неравенства можно умножить (разделить) на одно и то же положительное число, при этом получиться верное числовое неравенство; если же число отрицательное, то знак неравенства изменится на противоположный, т.е.:
если а < b и с > 0, то ac < bc;
если а < b и с < 0, то ac >bc.
Таким образом, если а < b, то: 2,5а < 2,5b (2,5 > 0),
а затем и 2,5а - 7 < 2,5b - 7.
ответ: 2,5а - 7 < 2,5b - 7.