
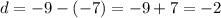
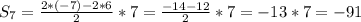
ответ:Чтобы разложить данные выражения на множители, надо преобразовать их в произведения, используя при этом формулы сокращенного умножения;
1) аb - 3 b + b^2 - 3 a, применим группировки;
(a b + b2) - (3 b + 3 a), из каждой скобки вынесем общий множитель;
b * (a + b) - 3 * ( b + a), теперь вынесем общий множитель выражения;
(a + b) * (b - 3).
2) 11 х - х у + 11 y - х^2, аналогично решению предыдущего примера, разложим на множители следующие выражения;
(11 x + 11 y) - (x^2 + x y) = 11 * (x + y) - x * (x + y) = (x + y) * (11 - x)
3) k n - m n - n^2 + m
Объяснение:
Объяснение:
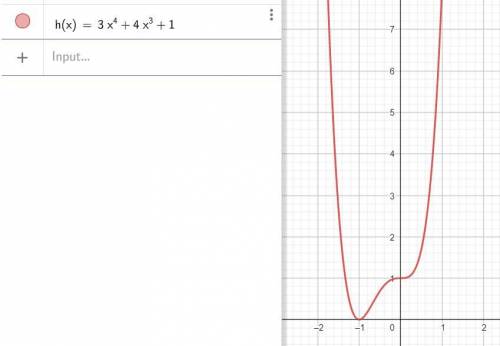
определяем производную
y'(x) = 12x³ + 12x² = 12x²(x+1)
y'(x) = 0 при
х1 = -1 - экстремум
х2 = 0 - экстремум
12x² всегда неотрицательно, как следствие:
y'(x) > 0 при х > -1
y'(x) < 0 при х < -1
у(х) убывает на х ∈ (-∞; -1)
у(х) возрастает на х ∈ (-1; 0) и (0; +∞)
х1 = -1 - экстремум - минимум
х2 = 0 - экстремум - перегиб
х ∈ (-∞; -1) - монотонно убывает
х ∈ (-1; 0) - монотонно возрастает
х ∈ (0; +∞) - монотонно возрастает
Точки для построения: в () - эксиремумы
х = {-2; (-1); -2/3; -1/2; -1/3; (0); 1/3; 2/3; 2}
y(-1) = 0;
y(0) = 1
остальные у - нужно посчитать
график - см. рис.
a7 = a1 + 6d = -7 - 12 = -19
S7 = (a1 + a7) / 2 = (-7 - 19)*7/2 = -13*7/2 = -91