Question

Решить уравнение: a) x^2 = корень из 19x^2-34 ; b) корень 4 степени из 25x^2-144 равно х

Answer 1

1)$x^2=\sqrt{19x^2-34}$

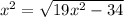
Область определения уравнения:

$19x^2-34 \geq 0$

$x \in (-\infty;-\sqrt{\frac{34}{19}}] \cup [\sqrt{\frac{34}{19}};+\infty)$

Возведем обе неотрицательные части в квадрат:

$x^4=19x^2-34$

$x^4-19x^2+34=0$

Решение подобного биквадратного уравнения сводится к замене вида: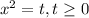$x^2=t,t \geq 0$

$t^2-19t+34=0$

$t_1=2;t_2=17$

Исходя из области определения корнями будут:

$x_1=-\sqrt{2};x_2=\sqrt{2};x_3=-\sqrt{17};x_4=\sqrt{17}$

ответ:$\{-\sqrt{17}\}\cup\{-\sqrt{2}\}\cup\{\sqrt{2}\}\cup\{\sqrt{17}\}$

$\sqrt[4]{25x^2-144}=x$

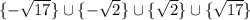
Область определения уравнения:

$25x^2-144 \geq 0$

$x\in(-\infty;-\frac{12}{5}] \cup [\frac{12}{5};+\infty)$

Преобразовывая область определения отбросим левую часть,так как корень равен неотрицательному числу(в данном случае числом является x,и при отрицательных x равенство не имеет место)

$x\in[\frac{12}{5};+\infty)$

Возведем обе неотрицательные части в четвертую степень:

$25x^2-144=x^4$

$x^4-25x^2+144=0$

Решение подобного биквадратного уравнения сводится к замене вида: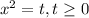$x^2=t,t \geq 0$

$t^2-25t+144=0$

$t_1=16;t_2=9$

Исходя из области определения корнями будут:

$x_1=3;x_2=4$

ответ:$\{3\} \cup \{4\}$