Объяснение:
Принимаем всю работу за единицу (1). ⇒
Скорость выполнения работы одним мастером равна 1/12.
Скорость выполнения работы тремя мастерами равна 3/12=1/4.
Скорость выполнения работы одним учеником равна 1/30.
Скорость выполнения работы учеников впятером равна 5/30=1/6. ⇒
Скорость выполнения работы, когда работают 3 мастера и 5 учеников
одновременно равна:
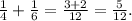
Таким образом, 3 мастера и 5 учеников работая вместе, выполнят работу за: 1:(5/12)=12/5=2,4 (дня).
ответ: 3 мастера и 5 учеников работая вместе,
выполнят работу за 2,4 дня.
1)Решение системы уравнений х=1
у=2
3)Решение системы уравнений х=1
у=1
5)Решение системы уравнений х=1
у=2
7)Решение системы уравнений х= -1
у=1
Объяснение:
1)2х+у=4
3х-2у= -1
Выразим у через х в первом уравнении, подставим выражение во второе уравнение и вычислим х:
у=4-2х
3х-2(4-2х)= -1
3х-8+4х= -1
7х= -1+8
7х=7
х=1
у=4-2х
у=4-2*1
у=2
Решение системы уравнений х=1
у=2
3)3х+у=4
5х+3у=8
Выразим у через х в первом уравнении, подставим выражение во второе уравнение и вычислим х:
у=4-3х
5х+3(4-3х)=8
5х+12-9х=8
-4х=8-12
-4х= -4
х=1
у=4-3х
у=4-3*1
у=1
Решение системы уравнений х=1
у=1
5)3х-у=1
2х+3у=8
Выразим у через х в первом уравнении, подставим выражение во второе уравнение и вычислим х:
-у=1-3х
у=3х-1
2х+3(3х-1)=8
2х+9х-3=8
11х=8+3
11х=11
х=1
у=3х-1
у=3*1-1
у=2
Решение системы уравнений х=1
у=2
7)3х+2у= -1
2х-у= -3
Выразим у через х во втором уравнении, подставим выражение в первое уравнение и вычислим х:
-у= -3-2х
у=3+2х
3х+2(3+2х)= -1
3х+6+4х= -1
7х= -1-6
7х= -7
х= -1
у=3+2х
у=3+2*(-1)
у=3-2
у=1
Решение системы уравнений х= -1
у=1
y=-x^2+2x+3
Найдем точки пересечения параболы с осью OX
-x^2+2x+3=0
x^2-2x-3=0
D=b^2-4ac=16
x1=3
x2=-1
S=int (-x^2+2x+3)dx от -1 до 3 = (-x^3/3+x^2+3x ) от -1 до 3 = 9-(-1 2/3)=10 2/3
2) y=-2*(x-3)^2+2
Найдем точки пересечения параболы с осью OX
-2*(x-3)^2+2=0
Сделаем замену t=x-3
-2t^2+2=0
t^2=1
t1=1
t2=-1
То есть
a) x-3=1 => x=4
б) x-3=-1 => x=2
тогда
s= int(-2*(x-3)^2+2)dx от 2 до 4 =(-2*(x-3)^3/3 +2x) от 2 до 4 =22/3 - 14/3 = 8/3 = 2 2/3