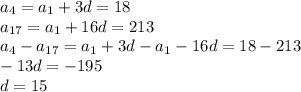
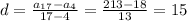
аналог lorem ipsum
прародителем текста-рыбы является известный "lorem ipsum" – латинский текст, ноги которого растут аж из 45 года до нашей эры. сервисов по созданию случайного текста на основе lorem ipsum великое множество, однако все они имеют один существенный недостаток: их "рыба текст" подходит лишь для ресурсов/проектов. мы же, фактически, предлагаем lorem ipsum на языке – вы можете использовать полученный здесь контент абсолютно бесплатно и в любых целях, не запрещенных законодательством. однако в случае, если сгенерированный здесь текст используется в коммерческом или публичном проекте, ссылка на наш сервис обязательна.
принцип работы генератора бредотекста
генерация рыбатекста происходит довольно просто: есть несколько фиксированных наборов фраз и словочетаний, из которых в определенном порядке формируются предложения. предложения складываются в абзацы – и вы наслаждетесь очередным бредошедевром.
сама идея работы генератора заимствована у псевдосоветского "универсального кода речей", из которого мы выдернули используемые в нем словосочетания, запилили приличное количество собственных, в несколько раз усложнили алгоритм, добавив новые схемы сборки, – и оформили в виде быстрого и удобного сервиса для получения тестового контента.
универсальный код речей
другое название – "универсальный генератор речей". по легенде, всякие депутаты и руководители в использовали в своих выступлениях заготовленный набор совмещающихся между собой словосочетаний, что позволяло нести псевдоумную ахинею часами. что-то вроде дорвеев для политсобраний.
кстати, "универсальный код речей" насчитывает только 40 таких словосочетаний, тогда как в нашем случае – их уже 192. из них наш генератор рыбатекста способен составить примерно 5 287 500 уникальных предложений-комбинаций (в оригинале же - только 10 000). просто вдумайтесь: около миллиарда символов случайного текста.
См. рисунок
1. Правильный шестиугольник, состоит из шести равносторонних треугольников.
Найдем сторону шестиугольника AB=r=48/6=8м.
Рассмотрим ΔСDO в нем CD=DO=0,5a (где а - сторона квадрата) ⇒ a=2CD
По теореме Пифагора найдем СD
r²=CD²+DO²=2CD² ⇒ r=CD√2⇒ м
м
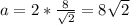 м
м
2. Из задачи №1. мы убедились, что радиус описанной окружности равен стороне правильного шестиугольника.
Площадь правильного шестиугольника равна
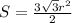 ⇒
⇒
 см
см
Длина окружности равна L=2πr=2π4√3=π*8√3≈43,5 см
3. Площадь сектора равна
 ≈151 см²
≈151 см²
(где n - градусная мера дуги сектора)
