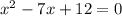
разложим с группировки
Рассмотрим x²+bx+c
. Найдем пару целых чисел, произведение которых равно c, а сумма равна b. В данном случае произведение равно 12, а сумма равна -7
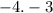
Запишем разложение на множители, используя эти целые числа.
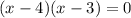
Если любой отдельный множитель в левой части уравнения равен 0 ,то и все выражение будет равняться 0.
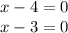
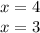
Используем каждый корень для создания проверочных интервалов.
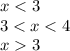
Выбираем тестовое значение из каждого интервала и подставляем его в начальное неравенство, чтобы определить, какие интервалы удовлетворяют неравенству.
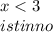
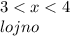
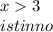
Решение включает все истинные интервалы.
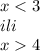
Результат можно выразить в различном виде.
Форма неравенства:
x < 3 или x > 4
Запись в виде интервала:
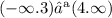
Объяснение:
Задание 1
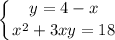
Значение у из первого уравнения подставим во второе уравнение
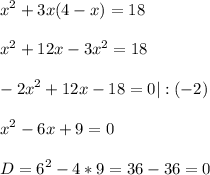
Если дискриминант равен нулю , то квадратное уравнение имеет только один действительный корень, также можно сказать , что квадратное уравнение имеет два действительных корня , которые равны между собой.
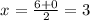

Задание 2
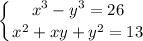
первое уравнение в системе это разность кубов, разложи на множители:
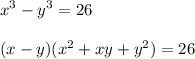
из второго уравнения подставим значение выражения х²+ху+у²
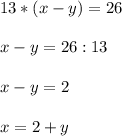
подставим значение х во второе уравнение системы :
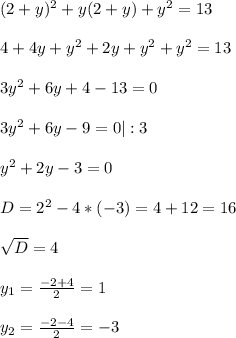
тогда
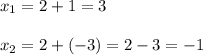
Корни уравнения ( 3 ;1) и ( -1 ; -3)
1) Разложим числитель и знаменатель дроби на множители
a² + 5a + 6 = a² + 2a + 3a + 6 = a(a+2) + 3(a+2) = (a+2)(a+3)
a² + 6a + 9 = (a+3)²
2) Снова же числитель и знаменатель дроби разложим на множители
5a² - 9a - 2 = 5a² - 10a + a - 2 = 5a(a-2) + a-2 = (a-2)(5a+1)
a² - 3a + 2 = a² - a - 2a + 2 = a(a-1) - 2(a-1) = (a-1)(a-2)