Найдите наименьшее значение многочлена p(x): p(x)=x в квадрате -5х+8 найдите наибольшее значение многочлена p(x): 7-x в квадрате -6х

👇

Ответ:

qwerty2569

15.02.2021

1) График функции парабола, ветви вверх, поэтому ее наим значение в вершине x вершины=-b/2a=5/2 , y вершины= (5/2)^2-5*5/2+8=7 - это и есть наименьшее значение.
2) график ф-ии - парабола, ветви вниз, наиб значение в вершине. Xв=-b/2a=6/(-2)=-3. Yв=-(-3)^2-6*(-3)+7=-9+18+7=16

4,6(58 оценок)

Открыть все ответы

Ответ:

Lenokin88

15.02.2021

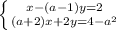
$\left \{ {{x-(a-1)y=2} \atop {(a+2)x+2y=4-a^2}} \right.$

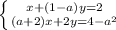
$\left \{ {{x+(1-a)y=2} \atop {(a+2)x+2y=4-a^2}} \right.$

Система эквивалентных уравнений имеет бесконечное количество решений, это означает, что отношения коэффициентов при неизвестных и свободных членов должны быть равны.

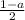$\frac{1}{a+2}$ отношения коэффициентов при

$\frac{1-a}{2}$ отношения коэффициентов при

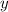
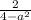$\frac{2}{4-a^2}$ отношения свободных членов

Получаем равенство.

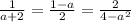
$\frac{1}{a+2} =\frac{1-a}{2} =\frac{2}{4-a^2}$

Решаем попарно.

1) Равенство первой и второй дробей

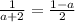
$\frac{1}{a+2} =\frac{1-a}{2}$

1*2=(1-a)((a+2)

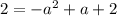
2=-a^2+a+2

a^2-a=0

a(a-1)=0

a_1=0; a_2=1

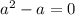
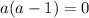
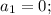
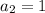
2) Равенство первой и третьей дробей

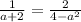
$\frac{1}{a+2} =\frac{2}{4-a^2}$

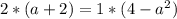
$2*(a+2) =1*({4-a^2)$

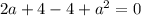
2a+4-4+a^2=0

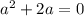
a^2+2a=0

a(a+2)=0

a_1=0; a_2=-2

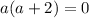
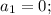
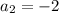
3) Равенство второй и третьей.

$\frac{1-a}{2} =\frac{2}{4-a^2}$

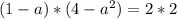
(1-a)*(4-a^2)=2*2

4-a^2-4a+a^3=4

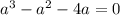
a^3-a^2-4a=0

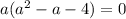
a(a^2-a-4)=0

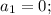
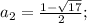
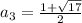
a_1=0; $a_2=\frac{1-\sqrt{17} }{2};$ $a_3=\frac{1+\sqrt{17} }{2}$

Общее решение: 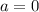a=0

ответ: при 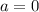a=0

4,7(80 оценок)

Ответ:

aptemacko

15.02.2021

Дана функция f(x) = x³ - 3x² + 12.
График функции пересекает ось X при f = 0
значит надо решить уравнение:
x³ - 3 x² + 12 = 0.
Решаем это уравнение
Точки пересечения с осью X:
Аналитическое решение даёт 2 комплексных и один действительный корень:
$x_1=- \frac{1}{3} \sqrt[3]{54 \sqrt{6}+135 }- \frac{3}{ \sqrt[3]{54 \sqrt{6} +135} } +1.$
Численное решение
x_{1} = -1,6128878.

График пересекает ось Y, когда x равняется 0:
подставляем x = 0 в x^3 - 3*x^2 + 12.
0^{3} - 0 + 12.
Результат:
f(0) = 12.
Точка:
(0, 12).

Для того, чтобы найти экстремумы, нужно решить уравнение
{d}{dx} f(x) = 0. (производная равна нулю), и корни этого уравнения будут экстремумами данной функции:
$$\frac{d}{d x} f{\left (x \right )} = $$
Первая производная
3x² - 6x = 0 или 3х(х - 2) = 0.
Решаем это уравнение.
Корни этого уравнения:
x_{1} = 0.
x_{2} = 2.
Значит, экстремумы в точках:
(0, 12)
(2, 8)

Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимумы функции в точках:
x_{2} = 2.
Максимумы функции в точках:
x_{2} = 0.
Убывает на промежутках (-oo, 0] U [2, oo).
Возрастает на промежутках [0, 2].

Найдем точки перегибов, для этого надо решить уравнение
{d^{2}}{d x^{2}} f(x ) = 0, (вторая производная равняется нулю),
корни полученного уравнения будут точками перегибов для указанного графика функции: {d^{2}}{d x^{2}} f(x) = 6х - 6.
Вторая производная 6(х - 1) = 0.
Решаем это уравнение.
Корни этого уравнения x_{1} = 1.

Интервалы выпуклости и вогнутости:
Найдём интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках перегибов:
вогнутая на промежутках [1, oo),
выпуклая на промежутках (-oo, 1].

Горизонтальные асимптоты найдём с пределов данной функции при x->+oo и x->-oo
\lim_{x \to -\infty}\left(x^{3} - 3 x^{2} + 12\right) = -∞.
Значит, горизонтальной асимптоты слева не существует.
\lim_{x \to \infty}\left(x^{3} - 3 x^{2} + 12\right) = ∞.
Значит, горизонтальной асимптоты справа не существует.

Наклонную асимптоту можно найти, подсчитав предел функции x^3 - 3*x^2 + 12, делённой на x при x->+oo и x ->-oo
$$\lim_{x \to -\infty}\left(\frac{1}{x} \left(x^{3} - 3 x^{2} + 12\right)\right) = ∞.
Значит, наклонной асимптоты слева не существует.
\lim_{x \to \infty}\left(\frac{1}{x} \left(x^{3} - 3 x^{2} + 12\right)\right) = ∞.
Значит, наклонной асимптоты справа не существует.

Проверим функци чётна или нечётна с соотношений f = f(-x) и f = -f(-x).
Итак, проверяем:
\^{3} - 3 x^{2} + 12 = - x^{3} - 3 x^{2} + 12
- Нет.
x^{3} - 3 x^{2} + 12 = - -1 x^{3} - - 3 x^{2} - 12
- Нет.
значит, функция не является ни чётной, ни нечётной.

График дан в приложении.

4,8(77 оценок)

Это интересно:

Кулинария-и-гостеприимство

18.06.2020

Замена бальзамическому уксусу - натуральные вкусовые альтернативы...

Компьютеры-и-электроника

26.07.2022

Как зарегистрироваться в Snapchat без проблем и быстро?...

Финансы-и-бизнес

24.01.2022

Как оформить возврат НДС на приобретенный товар в Таиланде...

Транспорт