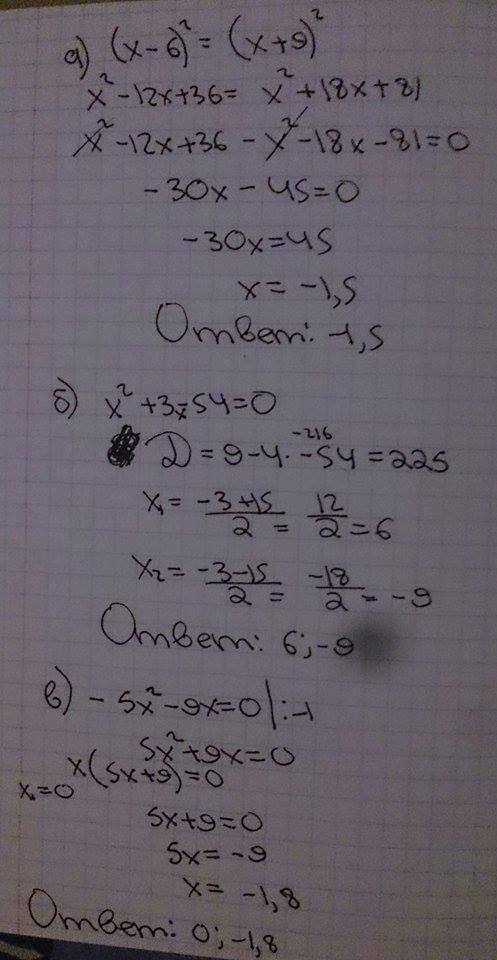
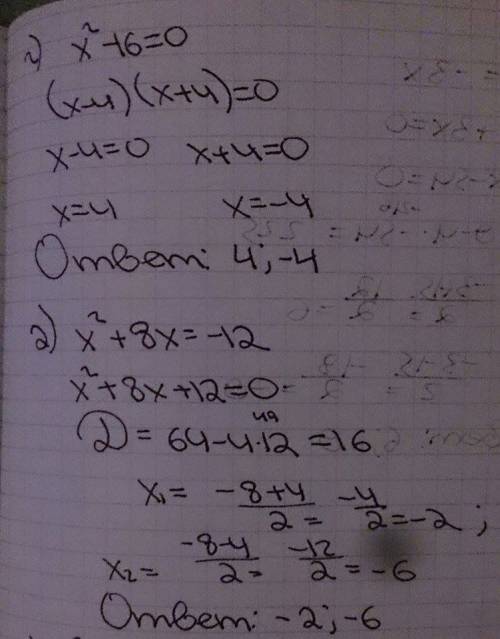
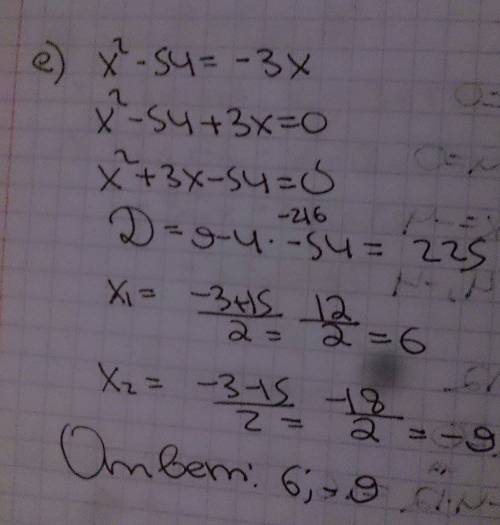
u₁=15 км/ч, u₂=10 км/ч, u₃=x км/ч, велосипедист = в-т
S₂=10·1=10 (км) - проехал второй в-т за 1 час.
К этому времени движение начал третий в-т и вскоре догнал второго со скоростью сближения равной x-u₂ км/ч, по времени это длилось:
t=S₂/(x-u₂)=10/(x-10) ч.
Всего третий в-т был в пути t₃=t+5=10/(x-10)+5 часов и за это время проехал путь S₃=u₃t₃=x·(10/(x-10)+5).
За всё время до встречи с третьим в-том первый в-т проехал:
S₁=u₁·2+u₁·t+u₁·5=u₁·(2+t+5)=15·(10/(x-10)+7). Так как 1 и 3 в-ты встретились, то пути, пройденные ими, равны:
S₁=S₃
15*(10/(x-10)+7)=x·(10/(x-10)+5)
10x/(x-10)+5x=150/(x-10)+105
(10x-150)/(x-10)=105-5x |·(x-10), x≠10
10x-150=(105-5x)(x-10)
10x-150=105x-1050-5x²+50x
5x²-145x+900=0
x²-29x+180=0
D=29²-4·1·180=841-720=121
x₁,₂=(-(-29)±√121)/(2*1)=(29±11)/2=20; 9 (км/ч)
x₂=9 км/ч не подходит, так как скорость третьего в-та должна быть больше и скорости первого, и скорости второго в-тов, так как он их догонял, тогда u₃=x₁=20 км/ч.
ответ: 20 км/ч
x^2 - 12x + 36 = x^2 + 18x + 81
x^2 - 12x + 36 - x^2 -18x - 81 = 0
-30x = 81 - 36
-30x = 45
x = -1,5
б) x^2+3-54=0
По Дискриминанту
D = b^2-4ac = 3^2 - 4*1*(-54) = 9+216=225
x1 = -b + √D/2a = -3 + 15/2 = 6
x2 = -b - √D/2a = -3 - 15/2 = -9
в) -5x^2-9x=0
x(-5x-9)=0
x=0 или -5x-9=0
-5x=9
x= -1,8
г) x^2-16=0
(x-4)(x+4)=0
x-4=0 или x+4=0
x = 4 x = -4
д) x^2+8x=-12
x^2+8x+12=0
По Дискриминанту
D = b^2-4ac = 8^2 - 4*1*12=64-48=16
x1 = -b + √D/2a = -8+4/2= -2
x2 = -b - √D/2a = -8-4/2= -6
е) x^2-54=-3x
x^2+3x-54=0
По Дискриминанту
D = b^2-4ac = 3^2-4*1*(-54)=9+216=225
x1 = -b + √D/2a = -3+15/2= 6
x2 = -b - √D/2a = -3-15/2=-9