давайте покажу два примера:
для решения задания нам для начала нужно знать теорему Виета
она выглядит вот так:
если наше квадратное уравнение выглядит так x² + px + q = 0, то
x1 + x2 = -p
x1 · x2 = q
судя по первому примеру -1+3=2
-1*3=-3
тогда наше уравнение будет выглядеть так х^2+2x-3=0
следущий пример точно также: -0,2+(-0,3)=-0,5
-0,2*(-0,3)=0,06
а уравнение-x^2-0.5x+0.06=0
Желаю удачи!
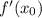производная функции в данной точке. А 
точка касания по иксу.
мы должны найти производную общего типа этой функции.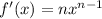
- где n это степень.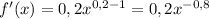
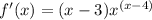
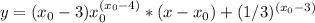
и получаешь уравнение касательной.
дробно-рациональная функция неопределена при значениях аргумента, при которых ее знаменатель обращается в 0,
x^2-1=0
x^2=1
x=1 или -1
поєтому ответ: a)-1;1