1) Находим y из первого уравнения 5y=1-6x y=(1-6x)/5 подставляем y во второе уравнение и решаем 2x-3((1-6x)/5)=33 2x-3/5+18x/5=33 2x-0.6+3.6x=33 5,6x=33+0.6 x=33.6/5.6 x=6 подставляем x в первое уравнение 6*6+5y=1 5y=1-36 y=-35/5 y=-7 проверяем 6*6+5*(-7)=1 36-35=1 1=1 ответ x=6, y=-7 2) Находим y из первогоуравнения 2-3x=2-2y -3x=-2y y=3x/2 подставляем y во второе уравнение 4(x+3x/2)=x-1.5 4x+6x=x-1.5 4x+6x-x=-1.5 9x=-1.5 x=-1.5/9 x=-0.17 2-3*(-0.17)=2-2y 2+0.51=2-2y 2y=2-2-0.51 y=-0.51/2 y=-0.255
1) Находим y из первого уравнения 5y=1-6x y=(1-6x)/5 подставляем y во второе уравнение и решаем 2x-3((1-6x)/5)=33 2x-3/5+18x/5=33 2x-0.6+3.6x=33 5,6x=33+0.6 x=33.6/5.6 x=6 подставляем x в первое уравнение 6*6+5y=1 5y=1-36 y=-35/5 y=-7 проверяем 6*6+5*(-7)=1 36-35=1 1=1 ответ x=6, y=-7 2) Находим y из первогоуравнения 2-3x=2-2y -3x=-2y y=3x/2 подставляем y во второе уравнение 4(x+3x/2)=x-1.5 4x+6x=x-1.5 4x+6x-x=-1.5 9x=-1.5 x=-1.5/9 x=-0.17 2-3*(-0.17)=2-2y 2+0.51=2-2y 2y=2-2-0.51 y=-0.51/2 y=-0.255
Найдем определитель матрицы:
![A=\left[\begin{array}{ccc}1&-2&-3\\4&1&2\\2&5&1\end{array}\right]](/tpl/images/0099/8716/e8b24.png)
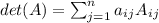
где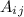
соответствующее алгебраическое дополнение
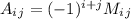
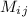 - минор матрицы А(получается удалением соответствующего столбца и строки)
- минор матрицы А(получается удалением соответствующего столбца и строки)
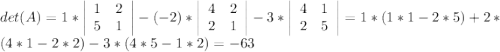
 ,такую,что первый столбец будет заменен на столбец из свободных членов.
,такую,что первый столбец будет заменен на столбец из свободных членов.
![A_1=\left[\begin{array}{ccc}-4&-2&-3\\13&1&2\\-7&5&1\end{array}\right]](/tpl/images/0099/8716/ad5cb.png)
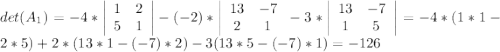
 ,такую,что второй столбец будет заменен на столбец из свободных членов.
,такую,что второй столбец будет заменен на столбец из свободных членов.
![A_2=\left[\begin{array}{ccc}1&-4&-3\\4&13&2\\2&-7&1\end{array}\right]](/tpl/images/0099/8716/a4542.png)
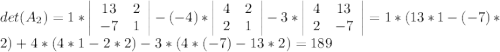
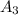 ,такую,что третий столбец будет заменен на столбец из свободных членов.
,такую,что третий столбец будет заменен на столбец из свободных членов.
![A_3=\left[\begin{array}{ccc}1&-2&-4\\4&1&13\\2&5&-7\end{array}\right]](/tpl/images/0099/8716/72fa0.png)
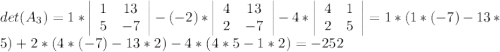
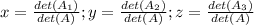
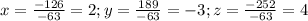
Построим матрицу
Построим матрицу
Построим матрицу
Согласну методу Крамера: