Объяснение:
1. a₁=-2 a₁₀=16 a₁₂=?
a₁₀=a₁+(10-1)*d=16
-2+9*d=16
9*d=18 |÷9
d=2 ⇒
a₁₂=a₁+(12-1)*d=-2+11*2=-2+22=20
ответ: а₁₂=20.
2. a₇=43 a₁₅=3 a₁₂=?
{a₇=a₁+6d=43
{a₁₅=a₁+14d=3
Вычитаем из нижнего уравнения верхнее:
8d=-40 |÷8
d=-5 ⇒
a₁+6*(-5)=43
a₁-30=43
a₁=73
a₁₂=73+11*(-5)=73-55=18
ответ: a₁₂=18.
3. a₁=30 d=-0,4 a₁₂=?
a₁₂=30+11*(-0,4)=30-4,4=25,6
ответ: a₁₂=25,6.
4. a₁₀=9,5 S₁₀=50 a₁₂=?
Sn=(a₁+an)*n/2
(a₁+9,5)*10/2=50
(a₁+9,5)*5=50 |÷5
a₁+9,5=10
a₁=0,5
a₁₀=a₁+9d=9,5
0,5+9d=9,5
9d=9 |÷9
d=1 ⇒
a₁₂=a₁+11d=0,5+11*1=0,5+11=11,5.
ответ: а₁₂=11,5.
первым делом нужно расписать уравнение так, как надо:
-х^2+4х-3
по графику видно, что функция убывающая, т.к. перед х^2 стоит минус, для нахождения его вершины есть особая формула, которую нужно выучить, она тебе не раз пригодится:
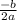 (обрати внимание: -b, это важно)
(обрати внимание: -b, это важно)
число b это число 4(потому что квадратное уравнение имеет вид aх^2+bx+c( в данном случае а=-1, b=4 и с=-3)
теперь подставим в формулу:
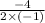
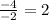
ответ: вершина параболы х=2, найдем у, просто подставив в уравнение: у=4*2-4-3=8-7=1
Получились координаты:(2;1)
(x+y)^2-2xy=25 xy=-12
x=-3; y=4 (-3;4)
x=4; y=-3 (4;-3)
ответ : { (-3;4), (4;-3)}