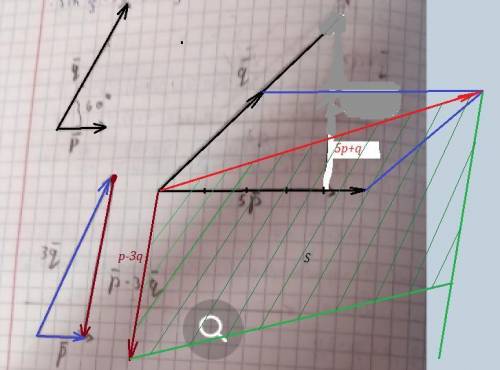
Вектор 5р : рисуем того же направления, что и вектор р, только в 5 раз длиннее.
Вектор q рисуем с параллельного переноса, совместив его начало с началом вектора 5р . Угол в 60 градусов сохраняется.
По правилу параллелограмма - диагональ параллелограмма, построенного на векторах 5р и q , является суммой этих векторов. Диагональ выходит из точки, являющейся общим началом векторов 5р и q .
Далее строим вектор 3q , длина которого в 3 раза больше длины вектора q , а направление совпадает с направлением вектора q .
Вектор ( р-3q ) - это сторона треугольника, соединяющая конец вектора 3q и начало вектора р . Причём векторы р и 3q имеют общее начало . Направление вектора (р-3q) идёт от вектора 3q к вектору р . На рисунке этот параллелограмм заштрихован зелёной штриховкой .
Чтобы построить параллелограмм, площадь которого равна векторному произведению векторов (5p+q) и (р-3q) , надо опять выбрать точку, которая будет началом как вектора (5р+q) , так и вектора (р-3q) . Затем достроить параллелограмм .
![(5p+q)\times (p-3q)=5[\, p\times p\, ]-15[\, p\times q\, ]+[\, q\times p\, ]-3[\, q\times q\, ]=\\\\=5\cdot 0-15[\, p\times q\, ]-[\, p\times q\, ]-3\cdot 0=-16[\, p\times q\, ]\\\\S=\Big |\, -16\cdot [\, p\times q\, ]\, \Big |=16\cdot |\, p\, |\cdot |\, q\, |\cdot sin60^\circ =16\cdot |\, p\, |\cdot |\, q\, |\cdot \frac{\sqrt3}{2}=\\\\=8\sqrt3\cdot |\, p\, |\cdot |\, q\, |](/tpl/images/1012/8562/61754.png)
Объяснение:
1) F(x) = √(4 - 5*x), Xo = 0
Y = F'(Xo)*(x - Xo) + F(Xo) - формула касательной.
Находим первую производную - k - наклон касательной.
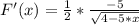
F'(Xo) = F'(0) = - 5/4 = k
F(0) = 2
y = - 5/4*x + 2 - касательная - ответ.
Задача 2)
ДАНО:Y(x) = x³ -3*x² + 2
ИССЛЕДОВАНИЕ.
1. Область определения D(y) ∈ R, Х∈(-∞;+∞) - непрерывная , гладкая.
2. Вертикальная асимптота - нет - нет разрывов.
3. Наклонная асимптота - y = k*x+b.
k = lim(+∞) Y(x)/x = +∞ - нет наклонной (горизонтальной) асимптоты.
4. Периода - нет - не тригонометрическая функция.
5. Пересечение с осью OХ.
Применим теорему Безу. х₁ *х₂ *х₃ = 2
Применим тригонометрическую формулу Виета.
Разложим многочлен на множители. Y=(x+0,73)*(x-1)*(x-2,73)
Нули функции: Х₁ =-0,73, Х₂ =1, Х₃ =2,73
6. Интервалы знакопостоянства.
Отрицательная - Y(x)<0 X∈(-∞;-0,73]U[1;2,73] Положительная -Y(x)>0 X∈[-0,73;1]U[2,73;+∞)
7. Пересечение с осью OY. Y(0) = 2
8. Исследование на чётность.
В полиноме есть и чётные и нечётные степени - функция общего вида.
Y(-x) ≠ Y(x) - не чётная. Y(-x) ≠ -Y(x), Функция ни чётная, ни нечётная.
9. Первая производная. Y'(x) = 3*x² -6*x = 0
Корни Y'(x)=0. Х₄ =0 Х₅=2
Производная отрицательна между корнями - функция убывает.
10. Локальные экстремумы.
Максимум - Ymax(X₄= 0) =2. Минимум - Ymin(X₅ = 2) =-2
11. Интервалы возрастания и убывания.
Возрастает Х∈(-∞;0;]U[2;+∞) , убывает - Х∈[0;2]
12. Вторая производная - Y"(x) = 6* x -6 = 0
Корень производной - точка перегиба Х₆=1
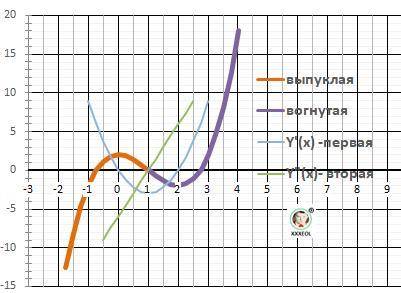
13. Выпуклая “горка» Х∈(-∞; Х₆ = 1]
Вогнутая – «ложка» Х∈[Х₆ = 1; +∞).
14. График в приложении.
Задача 3)
Ymin(0) = -3, Ymax(2) = 9 - ответ.
 : [tex]f(x)=\sqrt{4-5x} , x_{0} =0[/tex" />
: [tex]f(x)=\sqrt{4-5x} , x_{0} =0[/tex" />
3)f`(x)=39x²-7x
f`(0)=0
f`(-1)=39+7=46
f`(0)+f`(-1)=0+46=46
4)y`=-2x/2√(x²+1)³=-1/√(x²+1)³
5)y`=24(1/3x-64)^23 * 1/3=8(1/3x -64)^23
6)y`=1/cos²x
y`(π/3)=1/cos²π/3=1:1/4=4
7)tga=f`(x0)
f`(x)=6x²-5
f`(2)=6*4-5=24-5=19
tga=19
8)f(x)=x^8 -1
f`(x)=8x^7
9)y`=8cos3x*(-sin3x)*3=-24cos3xsin3x=-12sin6x
10)f(x)=1-4x²
f`(x)=-8x
f`(0,5)=-8*0,5=-4
11)y(1)=1+1=2
y`=4x³+1
y`(1)=4+1=5
Y=2+5(x-1)=2+5x-5=5x-3
12)f(1)=1
f`(x)=1/(2√x)
f`(1)=1/2
Y=1+1/2(x-1)=1+1/2x-1/2=1/2x+1/2
Y(31)=1/2*31+1/2=32*1/2=16
13)f`(x)=9-x²≥0
x²=9
x=+-3
_ + _
-3 3
x∈[-3;3]
14)(√x-4/√x)`=1/2√x +2/√x³=(x+4)/2√x³