8класс 1.докажите неравенство а)(х-3)^2 х(х-6) - id375471120221128 от клубничка114 28.11.2022 20:37

Question

Алгебра: 8класс 1.докажите неравенство а)(х-3)^2 х(х-6)

клубничка114 · Accepted Answer

Итак, ситуация номер 1 - имеется единственное решение:

Если 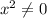$x^2\neq 0$ , то имеется либо 2 и более корней, либо их вообще нет.

Мы знаем, что x=0, тогда

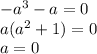
$-a^3-a=0\\a(a^2+1)=0\\a=0$

Решения для 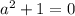a^2+1=0 просто откидываем, комплексные числа нам неинтересны.

Первая ситуация разобрана, но проверку стоит провести:

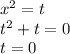
$x^2=t\\t^2+t=0\\t=0$

Второе решение 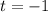t=-1 не подходит, т.к.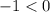

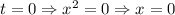
$t=0 \Rightarrow x^2=0 \Rightarrow x=0$

Проверка выполнена, имеется единственное решение при a=0

Вторая ситуация:

Необходимо 2 корня, значит значение t будет единственным!

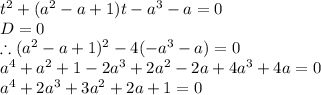
$t^2+(a^2-a+1)t-a^3-a=0\\D=0 \\\therefore (a^2-a+1)^2-4(-a^3-a)=0\\a^4+a^2+1-2a^3+2a^2-2a+4a^3+4a=0\\a^4+2a^3+3a^2+2a+1=0$

Данное уравнение не имеет решений, и при любом значении a D>0 (D по t).

Т.е. мы не имеем решений для второй ситуации.

Третья ситуация:

Т.к. D>0, то и в третьей ситуации удовлетворяющих значений a просто нет.

8класс 1.докажите неравенство а)(х-3)^2> х(х-6)