2) f(x) =x / 16 + x^2
У дроби знаменатель не должен никогда равнятся нулю, так как на ноль делить нельзя, поэтому
16+х^2 не равно 0
х^2 не равно 16
х не равен +-4
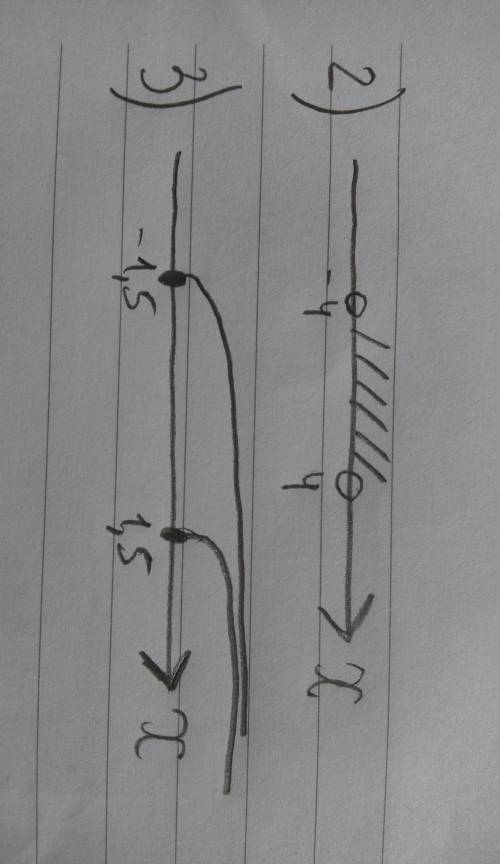
Тут надо нарисовать ось Х(забыла как называется), на ней отметить точки 4 и -4 и записать полученный интервал(будет на фото)
D(y)=(-4;4)-это ответ
3)f(x) =корень из х^2 – 2,25
Здесь работает другое правило:подкоренное выражение всегда больше или равно нулю.
х^2-2,25 больше или равно 0
х^2 больше или равно 2,25
х больше или равно +-1,5
Здесь тоже надо нарисовать ось Х, отметить полученные точки и написать ответ(будет на фото)
D(y) =(1,5;+бесконечности)
Привет! В первом если раскрыть скобки а^2 + ав -ав+в^2 = а^2+в^2
так как ав и -ав взаимо уничтожаются . Получается а^2+в^2
Во втором случае также а^2+ ав -ав - в^2= а^2-в^2
В примере 3 можно раскрыть скобки а^2 + ав + ав + в^2= а^2+2ав+в^2
Все примеры тождественно равны.
Есть еще формула квадрата суммы двух выражений
^2 - в квадрате
Объяснение:
Привет! В первом если раскрыть скобки а^2 + ав -ав+в^2 = а^2+в^2
так как ав и -ав взаимо уничтожаются . Получается а^2+в^2
Во втором случае также а^2+ ав -ав - в^2= а^2-в^2
В примере 3 можно раскрыть скобки а^2 + ав + ав + в^2= а^2+2ав+в^2
Все примеры тождественно равны.
Есть еще формула квадрата суммы двух выражений
^2 - в квадрате
2) непонятна запись - x^ 3 в числителе иди в знаменателе? Наверно, что-то пропущено
3) = 0,04 c^4 -n^6 = -n^6 + 0,04 c^4 ( по уменьшению степени)
4) 25/49 с^4 d^2 -81 ( двадцать пять сорок девятых умножить на c в 4-й умножить на d в квадрате)