{-3х+5у=4; {-3х+5у=4;
{2х+у=7; {у=7-2х;
-3х-5(7-2х)=4 31 31 29 (31 29)
х= --- = у=7-2* --- = у = --- = (х,у) (--- ,--- )
13 13 13 (13 13)
{ 31 29
{-3*---+5* = 4; (31 29
{ 13 13 {4=4; (х,у)= (--- , --- )
{ 31 29 {7=7; (13 13
{2*--- + = 7;
{ 13 13
Объяснение:
я надеюсь все понятно)
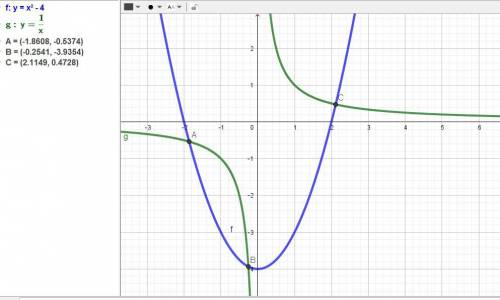
Дано уравнение x² - 4 = 1/x.
Умножим левую и правую части на х.
Получаем кубическое уравнение x³ - 4x - 1 = 0.
Решение таких уравнений производится по методам Виета или Кардано.
Решение данного уравнение по методу Виета приведено во вложении.
Можно применить числовые (итерационные) методы.
Один из них - метод половинного деления.
Сначала определяются значения функции при разных значениях аргумента. По знакам функции определяем промежутки, где имеются корни.
Далее находим значения функции по среднему значению аргумента между полученными положительным и отрицательным значениями функции.
И так производить вычисления, пока значение аргумента не даст с нужной точностью значения функции, близкое к нулю.
Ниже дано определение первого корня с точностью до 4 знаков.
х = -3 -2 -1 0 1 2 3
у = -16 -1 2 -1 -4 -1 14.
Как видим, имеются 3 корня в промежутках х = (-2;-1), (-1; 0) и (2; 3).
Находим первый.
x= -1,5 -1,75 -1,875 -1,8125 -1,84375 -1,859375 -1,8671875 -1,86328125 -1,861328125 -1,860351563 -1,860839844
y = 1,625 0,640625 -0,091796875 0,295654297 0,107330322 0,009128571 -0,04099226 -0,01584655 -0,003337689 0,002900763 -0,000217132.
Более точные значения корней:
х1 = -1,86081,
х2 = -0,254102,
х3 = 2,11491.

1)x²+4x+4>0⇒(x+2)²>0⇒x<-2 U x>-2
2)x²+4x+4≠1⇒x²+4x+3≠0
x1+x2=-4 U x1*x2=3
x≠-3 U x≠-1
3)x(x+1)(x+3)(x+4)>0
x=0 x=-1 x=-3 x=-4
+ _ + _ +
-4 -3 -1 0
x<-4 U -3<x<-1 U x>0
x∈(-∞;-4) U (-3;-2) U (-2;-1) U (0;∞)
a)x²+4x+4>1 при x∈(-∞;-4) U (0;∞)
log(x²+4x+4)(x(x+1)(x+3)(x+4))>1
x(x+1)(x+3)(x+4)>x²+4x+4
(x²+4x)(x²+4x+3)-(x²+4x+4)>0
x²+4x+3=a
(a-3)a-(a+1)>0
a²-3a-a-1>0
a²-4a-1>0
D=16+4=20 √D=2√5
a1=(4-2√5)/2=2-√5
a2=2+√5
a<2-√5 U a>2+√5
x²+4x+3<2-√5 U x²+4x+3>2+√5
1)x²+4x+(1+√5)<0
D=16-4-4√5=12-4√5
x1=(-4-2√(3-√5))/2=-2-√(3-√5) U x2=-2+√(3-√5)
(-2-√(3-√5)) <x<(-2+√(3-√5))
x∈(-∞;-4)/2) U (0;∞)
2)x²+4x+(1-√5)>0
D=16-4+4√5=12+4√5
x1=(-4-2√(3+√5))/2=-2-√(3+√5) U x2=-2+√(3+√5)
x<-2-√(3+√5) U x>-2+√(3+√5)
x∈(-∞;-2-√(3+√5)) U ((-2+√(3+√5);∞)
Общий x∈(-∞;-2-√(3+√5)) U ((-2+√(3+√5);∞)
б)x²+4x+4<1 при x∈(-3;-2) U (-2;-1)
log(x²+4x+4)(x(x+1)(x+3)(x+4))<1
a²-4a-1<0
2-√5<a<2+√5
x²+4x+3>2-√5 U x²+4x+3<2+√5
x<-2-√(3-√5) U x>-2+√(3-√5)
x∈(-3;-2-√(3-√5))U (-2+√(3-√5);-1)
ответ x∈(-∞;-4)/2) U -3;-2-√(3-√5))U (-2+√(3-√5);-1) U (0;∞)