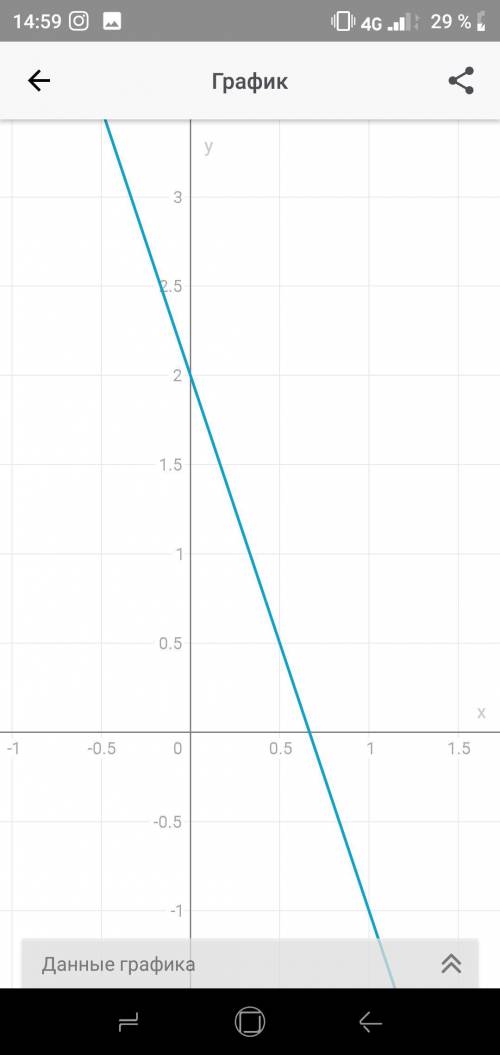
Ваш график
Объяснение:
Свойства ф-ции
1) Область определения функции - множество всех действительных чисел
2) Множеством значений функции является множество всех действительных чисел
3) Функция не имеет ни наибольшего, ни наименьшего значений.
4) Функция не является ни четной, ни нечетной (кроме особых случаев).
5) Функция непериодическая.
6) График функции пересекает ось Ох в точке , а ось Оу - в точке (0; b).
7) - является нулем функции.
8) Функция монотонно возрастает на области определения при k>0, монотонно убывает при k<0.
9) При k>0: функция принимает отрицательные значения на промежутке и положительные значения на промежутке
При k<0: функция принимает отрицательные значения на промежутке и положительные значения на промежутке
10) Коэффициент k характеризует угол, который образует прямая с положительным направлением Ох. Поэтому k называют угловым коэффициентом. Если k>0, то этот угол острый, если k<0 - тупой, если k=0, то прямая совпадает с осью Ох.
Если корни многочлена с меньшей степенью совпадают с корнями многочлена большей степени - то многочлен большей степени делится на многочлен меньшей степени
Для примера x^2 - 2x + 1 делится на x-1 (корень 1)
x-1=0 x=1
(x -1)^2 = 0 x=1
и не делится на х+1
Так и здесь найдем корни многочлена второй степени и подставим в многочлен 5-й степени, если и там будут корни, то значит делится, если нет - то не делится
x^2 - 3x - 18 = 0
D = 9 + 72 = 81
x12=(3+-9)/2 = 6 -3
(x+3)(x-6) = 0
подставляем найденные значения в x^5 − 4x^4 − 13x^3 + 216 = 0
1. х=-3
(-3)^5 - 4 *(-3)^4 - 13*(-3)^3 + 216 = -243 - 324 + 351 + 216 = - 567 + 567 = 0 да корень
2. х=6
6^5 - 4*6^4 - 13*6^3 + 216 = 7776 - 5184 - 2808 + 216 = 7992 - 7992 = 0
да корень
Значит многочлен пятой степени делится на многочлен второй степени без остатка
(x^5 − 4x^4 − 13x^3 + 216) / ( x^2 − 3x − 18) = x^3 - x^2 + 2x - 12
Б)a^3-3a^2*1+3a*1^2-1^3
B)a^3+6a^2+12a-8
Г)x^3-15x^2+75x-125
Д)a^6+3a^4*b^2+3a^2*b^4-b^6
E)a^9-3a^6*b^3+3a^3*b^6-b^9
Ж)1+4y^2+4y
3)4y^2+9-12y