Действительно, каким бы не было число а, (а²+3) всегда положительно, значит, не равно нулю. А коль так, то единственным корнем при любом а будет х= 5/(а²+3). Что и требовалось доказать.
Тут главная идея, делить можно на любое число, кроме нуля. Но (а²+3) никогда не равняется нулю. значит. на него можно делить.
Удачи!
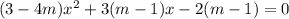
- переменная, а 
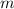- параметр.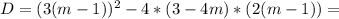
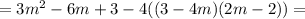
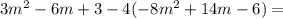
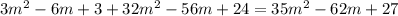
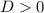будет два корня, которые не будут равны. При 
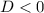корней не будет вообще, а при 
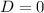- как раз то, что нужно! Ведь корень будет всего один (или, как говорят, корень второй кратности), а значит получится полный квадрат двучлена.
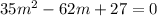. Заметим, что сумма коэффициентов равна нулю, а значит число 1 является корнем этого уравнения. По теореме Виета, другой корень будет равен 
.
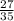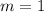и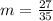 
наш трехчлен представляет собой полный квадрат.
Нехай (a^2+3) - це число = n, тоді:
n*x = 5
x = 5/n