Т.к отношение площадей треугольников равно квадрату коэффициента подобия, то к=3,а SАОD /SВОС=3^2, т.е 9.
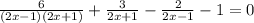
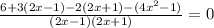
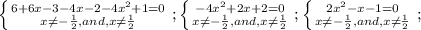
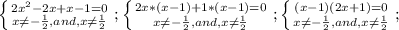
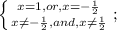
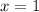
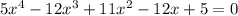
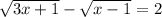
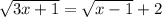 ,
, 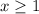
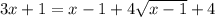 ,
, 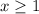
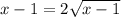 ,
, 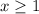
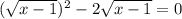 ,
, 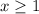
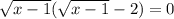 ,
, 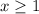
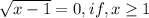
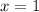
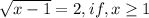
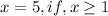
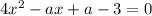
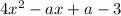 - парабола ветками вверх, нам нужен случай, когда вершина параболы лежит на оси ОХ, т.е. когда парабола пересекает эту ось в одной точке.
- парабола ветками вверх, нам нужен случай, когда вершина параболы лежит на оси ОХ, т.е. когда парабола пересекает эту ось в одной точке.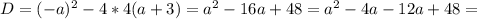
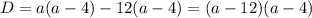
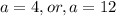
8а4 = 5 а n -2
8(a1 +3d) = 5( a1 + (n - 3)d)
8a1 +24 d = 5a1 +5d (n-3)
3a1 +24 d = 5d( n - 3)
9 +24 d = 5d(n-3) (*)
an = 3 + d(n-1)
3+ d( n -1) =15
d(n -1) = 12 ⇒ (n -1) = 12/d
Подставим в (*)
9 + 24d = 5d( n-1 -2)
9 + 24d = 5d(12/d -2)
9 + 24d = 5d·(12 -2d)/d
9 +24d = 5(12 -2 d)
9 + 24 d = 60 -10d
34 d = 51
d = 1,5
ответ: 3; 4,5; 6; 7,5; 9; 10,5; 12; 13,5; 15