Напишите уравнение касательной к графику функции y=x^2-x+3, которая параллельна прямой x+y+3=0

y=x^2-x+3; x+y+3=0

y=-x-3 k=-1

y'=2x-1

y=-x+l

2x-1=-1

x=0

y=3;3=-0+l; l=3 ответ: y=-x+3

Question

Алгебра: Напишите уравнение касательной к графику функции y=x^2-x+3, которая параллельна прямой x+y+3=0 буду признательна за ответ)

Evaliberman · Accepted Answer

Предположим, что х часов - это время работы первой бригады, тогда (х+4) часа - время работы второй бригады, примем всю работу за 1

согласно этим данным составим и решим уравнение для совместной работы:

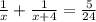$\frac{1}{x}+\frac{1}{x+4}=\frac{5}{24}$ /·24x(x+4)

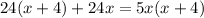
24(x+4)+24x=5x(x+4)

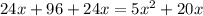
$24x+96+24x=5x^{2}+20x$

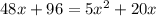
$48x+96=5x^{2}+20x$

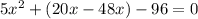
$5x^{2}+(20x-48x)-96=0$

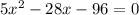
$5x^{2}-28x-96=0$

Cчитаем дискриминант:

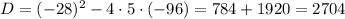
$D=(-28)^{2}-4\cdot5\cdot(-96)=784+1920=2704$

Дискриминант положительный

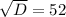
$\sqrt{D}=52$

Уравнение имеет два различных корня:

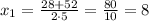
$x_{1}=\frac{28+52}{2\cdot5}=\frac{80}{10}=8$

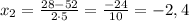
$x_{2}=\frac{28-52}{2\cdot5}=\frac{-24}{10}=-2,4$

не удовлетворяет условию задачи, так как отрицательное время быть не может

х=8 (ч) - I бригада.

х+4=8+4=12 (ч) - II бригада.

Следовательно, первая бригада заасфальтирует участок дороги за 8 часов, а вторая за 12 часов.

Напишите уравнение касательной к графику функции y=x^2-x+3, которая параллельна прямой x+y+3=0 буду признательна за ответ)