![\left[\begin{array}{ccc}2.5y-4=0\\6y-1.8=0\end]](/tpl/images/0379/9304/dffa5.png)
![\left[\begin{array}{ccc}y=1.6\\y=0.3\end]](/tpl/images/0379/9304/0fed4.png)
1) h =13m; 2) t =1+ √1,3+
Объяснение:
h = 18t - 5t²
вначале при полете вверх на камень действует сила тяжести, которая снижает его скорость до полной остановки, а затем он под действием силы тяжести вернется обратно на землю.
1) определим в какой момент времени камень брошенный вверх потеряет скорость (v=0)
v = v0 - gt ; v0-gt = 0
t = v0/g время подъема, t = 10/10 =1 c.
а теперь рассчитаем высоту на которую он поднимется
h = 18v0/g - 5(v0/g)² (для удобства расчета примем g=10)
h = 18*10/10 - 5(10/10)² =18 - 5 =13
h =13 m t = 1 время подъема
2)теперь определим время возврата мяча на землю под действием силы тяжести.
h = v0t + gt²; где v0=0 начальная скорость. g =10
h = gt²
t² = h/g
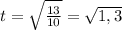время падения
полное время полета с момента запуска
t = t1 + t2 = 1 + √1.3
0,5+m
Объяснение:
Для того, чтобы найти требуемое значение логарифма log49(28), которого обозначим через L, воспользуемся следующей формулой loga(b / с) = logab / logaс (где а > 0, a ≠ 1, b > 0, c > 0), которая называется формулой перехода к новому основанию.
В нашем примере новым основанием будет число 7, так как дано log7(2) = m. Итак, имеем L = log7(28) / log7(49). Поскольку 28 = 7 * 22 и 49 = 72, то используя следующие формулы, преобразуем полученное выражение: loga(b * с) = logab + logaс (где а > 0, a ≠ 1, b > 0, c > 0) и logabn = n * logab (где а > 0, a ≠ 1, b > 0, n – любое число). Получим: L = log7(7 * 22) / log7(72) = (log7(7) + log7(22)) / log7(72) = (log7(7) + 2 * log7(2)) / (2 * log7(7)).
Очевидно, что log7(7) = 1. Тогда, имеем: L = (1 + 2 * m) / (2 * 1) = 1 : 2 + 2 * m : 2 = 0,5 + m.
