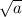 . Эта система будет иметь единственное решение только тогда, когда эти окружности касаются. Они могут касаться внешним или внутренним образом. Наименьшее значение
. Эта система будет иметь единственное решение только тогда, когда эти окружности касаются. Они могут касаться внешним или внутренним образом. Наименьшее значение  будет при внешнем касании, когда сумма радиусов равна расстоянию между центрами. Расстояние между центрами равно
будет при внешнем касании, когда сумма радиусов равна расстоянию между центрами. Расстояние между центрами равно 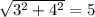 . Значит, искомое
. Значит, искомое  получится из условия
получится из условия 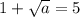 , т.е. a=16. ответ: Б.
, т.е. a=16. ответ: Б.