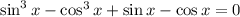
Воспользуемся формулой разности кубов:
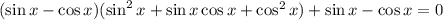
Выносим за скобки общий множитель:
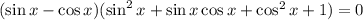
Уравнение распадается на два. Решаем первое:
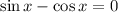
Почленно разделим на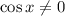 
:
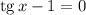
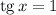
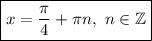
Решаем второе уравнение:
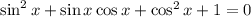
Заметим в левой части основное тригонометрическое тождество:
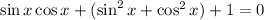
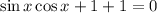
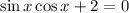
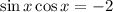
Обе части уравнения домножим на 2:
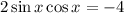
Чтобы в левой части применить формулу синуса двойного угла:
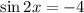
Но так как синус любого угла принимает значения только из отрезка от -1 до 1, то последнее уравнение не имеет решение.
Значит, никаких других корней, кроме найденных ранее, исходное уравнение не имеет.
ответ: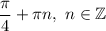 
1.
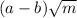
Если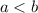 
, то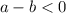 
. Но внести под знак корня мы можем только неотрицательный множитель. Тогда, преобразуем следующим образом:
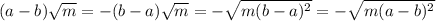
2.
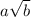
Аналогично, необходимо рассмотреть два случая:
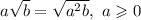
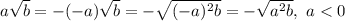
3.
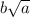
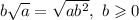
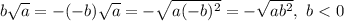
Уточнение. Если условие 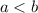относится и к двум последним примерам тоже, то для второго примера оно не никак. А для третьего примера на основе него можно сделать вывод, что множитель перед корнем больше числа, стоящего под знаком корня. Но поскольку под корнем стоит заведомо неотрицательное число, то и множитель перед корнем также неотрицателен. Тогда однозначно 
.
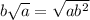