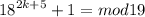
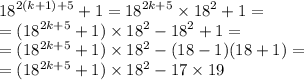
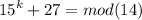
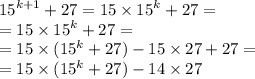
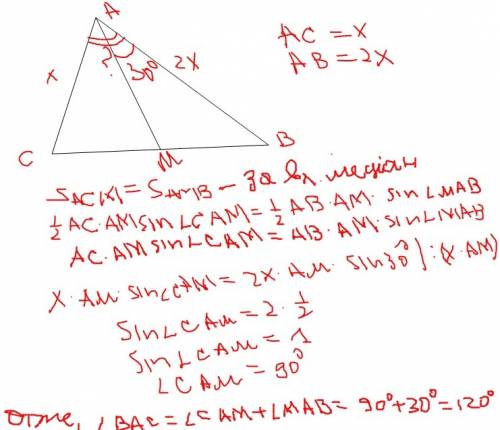
медиана делит треугольник на два равновеликих треугольника (у них площади равны): 0.5*АВ*АМ*sin(30°) = 0.5*AC*AM*sin(x)
2АC*(1/2) = AC*sin(x)
sin(x) = 1 ---> угол МАС = 90° ---> угол ВАС = 90°+30° = 120°
оказывается, очень мучиться не пришлось...
и второе решение даже изящное получилось))
если продолжить медиану на ее же длину, то треугольник достроится до параллелограмма... в получившемся треугольнике ABD "легко" заметить, что сторона против угла в 30° равна половине другой стороны... это верно только для прямоугольного треугольника)) и ∠BDA=∠CAD как накрест лежащие при параллельных АС и BD и секущей AD...
д=16-4*4*(-3)=16+16*3=√64=8
x1=4+8/2*4=12/8=1,5
x2=4-8/2*4=-4/8=-1/2.