a)7m-m^4
Выносим общий множитель за скобку
ответ: m(7-m^3)
б) 4a^2-24ab+36b
Выносим общий множитель за скобку
4(a^2-6ab+9^2)
Воспользуемся формулой квадрата разности
ответ: 4(a-3b)^2
в) pb-pc+6b-6c = (b-c)p+(6b-6c)
Выносим общий множитель
(b-c)p+(b-c)6=(b-c)(p+6)
ответ: (b-c)(p+6)
Уравнение:
x^3+125+5x(5+x)=0
Производим группировку
(x^3+125)+5x(5+x)=0
Воспользуемся формулой суммы кубов
(x^2-5x+25)(x+5)+(5x)(x+5)=0
Выносим общий множитель
((x^2-5x+25)+5x)(x+5)=0
Раскрываем скобки
(x^2-5x+25+5x)(x+5)=0
Приводим подобные члены
(x^2+25)(x+5)=0
Уравнение равно нулю если хотя бы один из множителей равен нулю
x^2+25=0
x^2=-25
корня нет
x+5=0
x=-5
ответ: x=-5
Преобразование:
а) (7a+b)(7a-b)-(b-4a)(4a+b)
Выносим знак минуса
(7a+b)(7a-b)+(4a-b)(4a+b)
Воспользуемся формулой разности квадратов
(49a^2-b^2)+(16a^2-b^2)
Раскрываем скобки и приводим подобные члены
65a^2-2b^2
ответ: 65a^2-2b^2
(3;2)
Объяснение:
Докажем сначала, что если x и y - натуральные числа и удовлетворяют этому уравнению (кстати, это частный случай диофантова уравнения, которое называют уравнением Ферма или уравнением Пелля), то либо x либо y делятся на 3 (точнее, ровно одно из них делится на 3, но для нашего решения это не важно). В самом деле, если x и y не делятся на 3, то
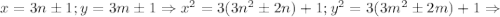
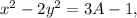то есть не может равняться 1. (число A получилось после вынесения общего множителя 3).
Итак, x или y делится на 3. Но по условию x и y - простые, поэтому x или y
равен 3.
1-й случай. 
Поскольку 2 - простое число, получили решение (3;2).
2-й случай.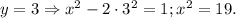 
Такое уравнение не имеет решений в целых числах.
x*x-x*7-3*x+3*7-2x*3x+2x*5. √
x²-7x-3x 8a -6x²+1Ox
5x²-11x
Б)4а*(а-2)-(а-4)^2
4a*a-4a*2-a²-2*a*4 +4² √
4a²-8a³- 8a +16
В)2(m+1)(в квадрате)-4m ×