Відповідь:
Шість головних діагоналей дорівнюють подвоєній стороні шестикутника.
Шість додаткових діагоналей дорівнюють стороні шестикутника помноженій на корень квадратний із трьох.
Пояснення:
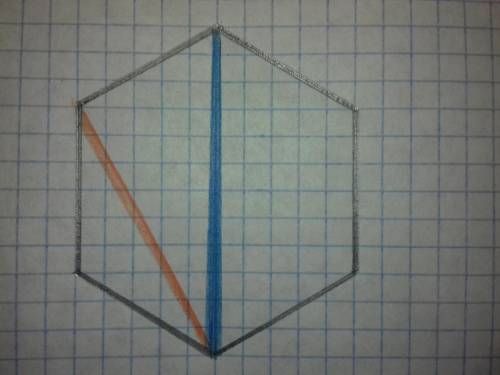
У правильному шестикутнику є шість головних діагоналей, що проходять крізь його геометричний центр ( центр описаної та вписаної окружності ), одна з них намальована синім кольором на малюнку. Довжина цієї діагоналі дорівнює подвоєній стороні шестикутника. Тому, що у правильному шестикутнику сторона дорівнює радіусу описаної окружності, а діагональ дорівнює двом радіусам.
Існує ще шість додадкових діагоналей, що не проходять крізь центр шестикутника, одна з таких діагоналей намальована червоним кольором на малюнку. Довжина такої діагоналі дорівнює стороні шестикутника помноженій на корень квадратний із трьох. Тому, що ця діагональ утворює рівнобічний трикутник з кутом при основі 30°, а основа трикутника дорівнює стороні шестикутника помноженій на 2 × cos (30°) = sqrt (3).
Оба этих уравнения являются уравнениями окружности.
Общее уравнение окружности:
где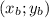 -координаты вершины окружности, R-радиус
-координаты вершины окружности, R-радиус
a)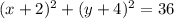
(-2;-4)-вершина, R=6
В системе координат отмечаем точку с координатами (-2;-4) и чертим окружность с центром в этой точке радиусом равным 6. Это и есть график нашей функции.(Совет-выбрать единичный отрезок равный 1 клеточке тетради)
б)[ tex]x^{2}+(y-1)^{2}=2,25[/tex]
(0;1)-вершина, R=1,5
В системе координат отмечаем точку с координатами (0;1)) и чертим окружность с центром в этой точке радиусом равным 1,5. Это и есть график нашей функции.(Совет-выбрать единичный отрезок равный двум клеточкам тетради)