1. У равнобедренного треугольника углы при основании равны, поэтому угол при основании не может быть равен 108°, значит угол при вершине равнобедренного треугольника равен 108°, тогда углы при основании:
α = (180° - 108°)/2 = 36°
ответ: 36°.
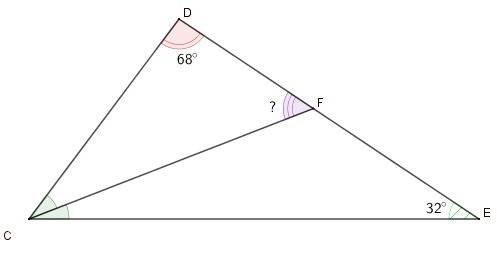
2) Полное условие. В треугольнике CDE проведена биссектриса CF, угол D=68*,угол E=32*. Найдите угол CFD.
Сумма внутренних углов треугольника равна 180°, поэтому
∠C = 180° - (∠D + ∠E) = 180° - (68°+32°) = 100°
Так как CF - биссектриса, то ∠DCF = ∠FCE = 0.5∠C = 50°
Рассмотрим треугольник CDF: ∠CFD = 180° - (∠CDF + ∠DCF)=62°
ответ: 62°
1. У равнобедренного треугольника углы при основании равны, поэтому угол при основании не может быть равен 108°, значит угол при вершине равнобедренного треугольника равен 108°, тогда углы при основании:
α = (180° - 108°)/2 = 36°
ответ: 36°.
2) Полное условие. В треугольнике CDE проведена биссектриса CF, угол D=68*,угол E=32*. Найдите угол CFD.
Сумма внутренних углов треугольника равна 180°, поэтому
∠C = 180° - (∠D + ∠E) = 180° - (68°+32°) = 100°
Так как CF - биссектриса, то ∠DCF = ∠FCE = 0.5∠C = 50°
Рассмотрим треугольник CDF: ∠CFD = 180° - (∠CDF + ∠DCF)=62°
ответ: 62°

обозн B₁C₁=x .
h² = 17² - ((44 - x)/2)² =39²- ((44+x)/2)² ;
34² -(44-x)² =78² - (44+x)² ;
(44+x)² - (44-x)² =78² -34² ;
2x*88=(78 -34)*(78+34) ;
2*88*x =44*112 ⇒ x= 28 ;
h²= 17² -((44-28)/2)² =289 -64=225 ⇒h=15
S(AB₁C₁D)= (AD +B₁C₁)/2*h =(44+28)/2*15=36*15=540.
S(AB₁C₁D) =S(ABCD)*cos60° ⇒S(ABCD) =1080.