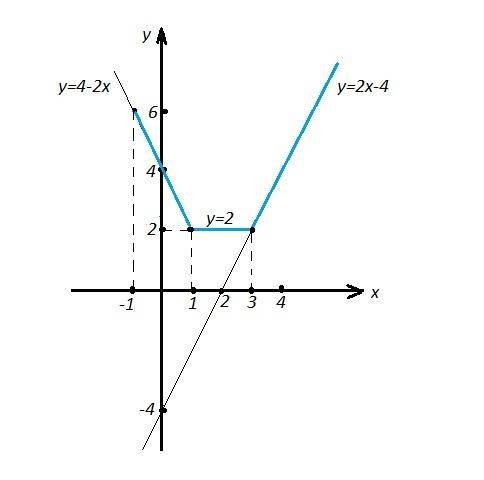
y=|x-1|+|x-3| , x≥ -1
Отметим нули выражений, находящихся под знаками модулей. Это х=1 и х=3. Вычислим знаки выражений, находящихся по знаками модулей, в трёх получившихся промежутках:
(х-1) : - - - (1) + + + (3) + + +
(х-3) : - - - (1) - - - - (3) + + +
Теперь рассмотрим, какой вид примет функция , в этих трёх промежутках.
1) -1≤ х≤1 : |x-1|=-(x-1)=1-x , |x-3|=-(x-3)=3-x ⇒ y=1-x+3-x , y=4-2x .
Cтроим прямую у=4-2х на промежутке х∈[-1, 1 ] .
2) 1<x≤3 : |x-1|=x-1 , |x-3|=-(x-3)=3-x ⇒ y=x-1+3-x , y=2.
Строим прямую у=2 на промежутке х∈(1,3 ] .
3) x>3 : |x-1|=x-1 , |x-3|=x-3 ⇒ y=x-1+x-3 , y=2x-4 .
Строим прямую у=2х-4 на промежутке х∈(3,+∞) .
График нарисован синим цветом на рисунке.
Объяснение:
(x^2+4x+16)^2+5x(x^2+4x+16)+4x^2
решим как квадратное относительно (x^2+4x+16)
D=25x²-4*4x²=9x²=(3x)²
1)x^2+4x+16=(-5x-3x)/2=-4x
2)x^2+4x+16=(-5x+3x)/2=-x
(x²+4x+16+4x)(x²+4x+16+x)=(x²+8x+16)(x^2+5x+16)=(x+4)(x+4)(x²+5x+16)
(x^2+x+1)^2+3x(x^2+x+1)-18x^2
решим как квадратное относительно (x^2+x+1)
D=9x²+4*18x²=81x²=(9x)²
1)x^2+x+1=(-3x-9x)/2=-6x
2)x^2+x+1=(-3x+9x)/2=3x
(x^2+x+1)^2+3x(x^2+x+1)-18x^2=
(x^2+x+1+6x)(x^2+x+1-3x)=(x^2+7x+1)(x^2-2x+1)=(x^2+7x+1)(x+1)(x+1)
D=49-4=45=9*5
x₁=(-7-3√5)/2
x₂=(-7+3√5)/2
(x^2+7x+1)(x+1)(x+1)=(x+1)(x+1)(x+(7+3√5)/2)(x-(-7+3√5)/2)
Выпадение одинаковых очков:
Вероятность того, что на обеих костей выпадет одинаковое число очков равно
А если выпадает разное число очков, то искомая вероятность: