a)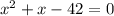 
Ищем дискриминант:
D=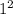
-4*1*(-42)=1-4*(-42)=1-(-4*42)=1-(-168)=1+168=169;
Дискриминант больше 0, уравнение имеет 2 корня: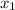
=
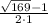=(13-1)/2=12/2=6;
= 
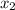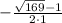=(13-1)/2=12/2=6 =(-13-1)/2=-14/2=-7.
б)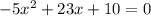 
Ищем дискриминант:
D=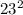
-4*(-5)*10=529-4*(-5)*10=529-(-4*5)*10=529-(-20)*10=529-(-20*10)=529-(-200)=529+200=729;
Дискриминант больше 0, уравнение имеет 2 корня: =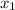 
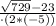=(27-23)/(2*(-5))=4/(2*(-5))=4/(-2*5)=4/(-10)=-4/10=-0.4;
= 
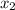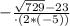=-50/(2*(-5))=-50/(-2*5)=-50/(-10)=-(-50/10)=-(-5)=5.
в)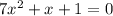 
Ищем дискриминант:
D=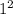-4*7*1=1-4*7=1-28=-27;
Дискриминант меньше 0, уравнение не имеет корней.
г)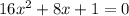 
Ищем дискриминант:
D=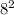 
-4*16*1=64-4*16=64-64=0;
Дискриминант равен 0, уравнение имеет 1 корень:
X=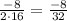
=-0.25
5sin²x + 3sinx × cosx - 4 = 0
5sin²x + 3sinx × cosx - 4×1 = 0
5sin²x + 3sinx × cosx - 4(sin²x + cos²x) = 0
5sin²x + 3sinx × cosx - 4sin²x - 4cos²x = 0
sin²x + 3sinx × cosx - 4cos²x = 0 | : cos²x
tg²x + 3tgx - 4 = 0
Пусть tgx = a, тогда:
a² + 3a - 4 = 0
D = 3² - 4×1×(-4) = 9 + 16 = 25
D>0, 2 корня
x₁ = -3+√25/2×1 = -3+5/2 = 2/2 = 1
x₂ = -3-√25/2×1 = -3-5/2 = -8/2 = -4
tgx = 1 или tgx = - 4
x₁ = π/4 + πn, n∈Z x₂ = arctg(-4) + πn, n∈Z
x₂ = - arctg 4 + πn, n∈Z
ответ: x₁ = π/4 + πn, n∈Z
x₂ = - arctg 4 + πn, n∈Z
Находим точку, в которой модуль превращается в ноль:
5-2х=0 х=2,5.
Эта точка разделяет действительную ось на интервалы:
(-∞;2,5)∨2,5;+∞).
Обозначаем знаки модульных функций на найденных интервалах (знаки определяем простой подстановкой точек из интервала:
х∈(-∞;2,5) +
х∈(2,5;+∞) -.
Раскрываем модуль, учитывая знаки и находим решение:
5-2х>7 x<-1
-5+2x<7 x>6.
Таким образом, интервалы (-∞;-1)∨(6;+∞) являются решением этого неравенства.
2) ΙхΙ+Ιх+3Ι<5
Находим точки, в которых модуль превращается в ноль;
х=0 х+3=0 х=-3.
Две точки разделяют действительную ось на интервалы:
(-∞;-3)∨(-3;0)∨(0;+∞).
Обозначаем знаки модульных функций на найденных интервалах:
(-∞;-3) - -
(-3;0) - +
(0;+∞) + +.
Раскрываем модули, учитывая знаки и находим решение:
-x-x-3<5 x>-4
-x+x+3<5 3<5 x∈(-∞;+∞)
x+x+3<5 x<1.
Таким образом, интервал (-4;1) является решением этого неравенства.