Объяснение:
15.6
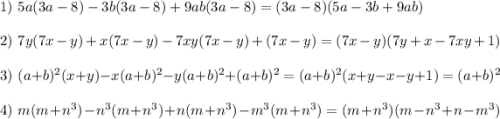
Выносим общую скобку как множитель.
15.9
Тут необходимо сначала разложить на множители, а затем воспользоваться правилом:
Если произведение двух или более множителей равно 0, то хотя бы один из множителей равен 0.
1)
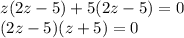
Произведение двух множителей равно 0, значит или 1 множитель равен 0, или второй множитель равен 0.
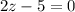 или
или 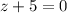
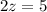 или
или 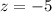
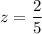 или
или 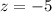
Мы решили! Это и есть ответ!
2)
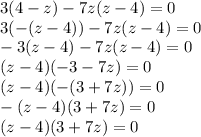
Произведение двух множителей равно 0, значит или 1 множитель равен 0, или второй множитель равен 0.
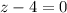 или
или 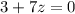
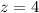 или
или 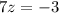
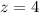 или
или 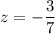
Мы решили! Это и есть ответ!
3)
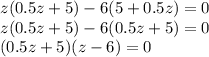
Произведение двух множителей равно 0, значит или 1 множитель равен 0, или второй множитель равен 0.
 или
или 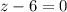
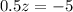 или
или 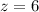
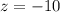 или
или 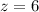
Мы решили! Это и есть ответ!
4)
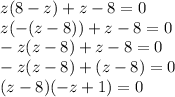
Произведение двух множителей равно 0, значит или 1 множитель равен 0, или второй множитель равен 0.
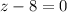 или
или 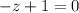
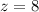 или
или 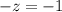
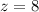 или
или 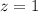
Мы решили! Это и есть ответ!
Объяснение:
15.6
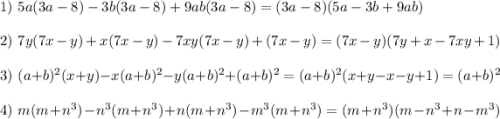
Выносим общую скобку как множитель.
15.9
Тут необходимо сначала разложить на множители, а затем воспользоваться правилом:
Если произведение двух или более множителей равно 0, то хотя бы один из множителей равен 0.
1)
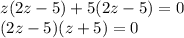
Произведение двух множителей равно 0, значит или 1 множитель равен 0, или второй множитель равен 0.
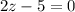 или
или 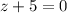
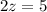 или
или 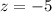
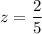 или
или 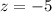
Мы решили! Это и есть ответ!
2)
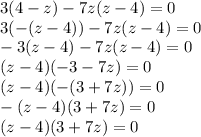
Произведение двух множителей равно 0, значит или 1 множитель равен 0, или второй множитель равен 0.
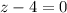 или
или 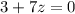
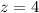 или
или 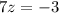
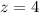 или
или 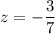
Мы решили! Это и есть ответ!
3)
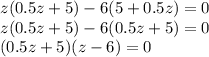
Произведение двух множителей равно 0, значит или 1 множитель равен 0, или второй множитель равен 0.
 или
или 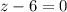
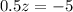 или
или 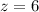
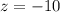 или
или 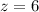
Мы решили! Это и есть ответ!
4)
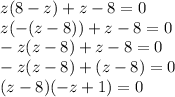
Произведение двух множителей равно 0, значит или 1 множитель равен 0, или второй множитель равен 0.
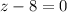 или
или 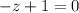
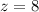 или
или 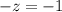
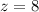 или
или 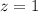
Мы решили! Это и есть ответ!
Находим точки, в которых модули превращаются в ноль:
х-1=0 х=1 х+3=0 х=-3.
Обе точки разделяют действительную ось на интервалы:
(-∞;-3)∨(1;+∞).
Обозначаем знаки подмодульных функций на найденных интервалах (знаки устанавливаем простой подстановкой точек из интервала:
(-∞;-3) - -
(-3;1) - +
(1;+∞) + +
Раскрываем модули, учитывая знаки и находим решение:
-х+1-х-3=6,2 -2х=8,2 х=-4,1
-х+1+х+3=6,2 х∉ (нет решения)
х-1+х+3=6,2 2х=4,2 х=2,1
ответ: х₁=-4,1 х₂=2,1.