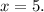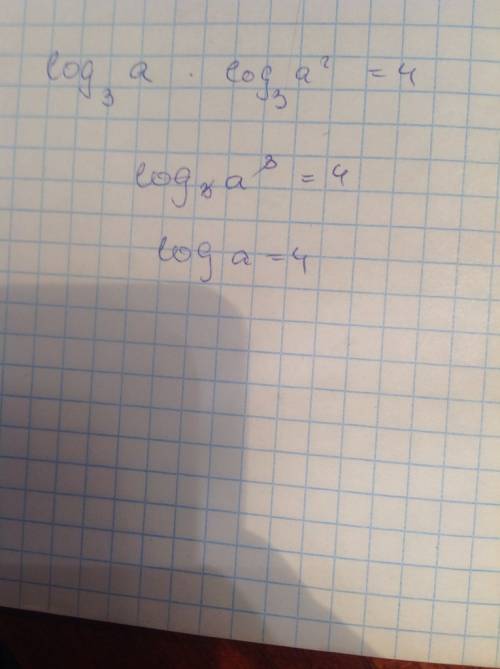
Главный герой произведения – русский офицер Жилин, служивший на Кавказе. По происхождению он являлся обнищавшим дворянином, однако, несмотря на это, был честен, имел добрую душу и чистые намерения. Ростом он был невысок, но достаточно силен. Пожилая мать героя просит навестить ее и тот отправляется к ней вместе с обозом, взяв отпуск. И на пути попадает в плен к татарам, захватившим его с целью выкупа. Происходит это по вине его товарища, офицера Костылина, который проявив невообразимую трусость покидает Жилина, забрав с собой ружьё.
Находясь в плену, Жилин был продан Абдулу, с чьей дочерью – обаятельной девочкой Диной, с течением времени, подружился, вылепливая для нее кукол из глины. Девочка, в ответ, по мере сил и возможностей ему, приносив еду, такую как лепешки, мясо и молоко. Жилину удается наладить взаимоотношения с татарами: он то и дело занимается работой, присматриваясь к людям, и на итог, в сарае его запирают лишь на ночь, поскольку ему удается завоевать доверие татар.
Костылин же, грузный мужичок из богатой помещичьей семьи, отличившийся своей трусостью, также был пойман в плен и попал к тому же хозяину, что и Жилин.
Толстой весьма красноречиво указывает нам на контраст между этими двумя героями. Волевой, мужественный, находчивый Жилин и пассивный, эгоистичный и обделенный умом Костылин. И несмотря на эти явные различия, на протяжении всего рассказа Жилин действительно пытался своему товарищу. Сделав подкоп под сараем, герои намереваются совершить побег, но по вине Костылина терпят неудачу.
Не заботясь о собственной судьбе, на Жилину, в очередной раз, приходит дочь хозяина Дина. Много миль преодолевает Жилин с оковами на ногах, прежде чем встречается с солдатами и казаками.
Однако, основная мысль этого произведения не только лишь в том, чтобы показать пример Жилина как положительного героя и акцентировать внимание на том факте, что всем нам следует брать с него пример, но и в том, насколько глупа и бесчеловечна была Кавказская война, ведь по обе стороны враждующих народов есть как плохие, так и хорошие люди.
Источник: Сочинение по рассказу Кавказский пленник Толстого 5 класс
![+ , - , \cdot , : , x^n , \sqrt[n]{x} и \log_a{x}](/tpl/images/0480/8307/7c93b.png) – имеют ОДНОЗНАЧНЫЙ результат. Вы, возможно знаете пока не все из них, но это не меняет ничего в рассуждениях. Однозначность действия означает, что при вычислении результата любого из них получается однозначный ответ. Ну, например, ведь нет такого, что у одного при вычислении
– имеют ОДНОЗНАЧНЫЙ результат. Вы, возможно знаете пока не все из них, но это не меняет ничего в рассуждениях. Однозначность действия означает, что при вычислении результата любого из них получается однозначный ответ. Ну, например, ведь нет такого, что у одного при вычислении 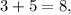 а у другого
а у другого 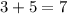 :–) ?! Конечно же, нет, это бы вызывало полную неразбериху и ни в одной науке ничего нельзя было бы вычислить ни по одной формуле. Но иногда, при изучении квадратного корня, учащиеся понимают это действие не совсем корректно, полагая, что
:–) ?! Конечно же, нет, это бы вызывало полную неразбериху и ни в одной науке ничего нельзя было бы вычислить ни по одной формуле. Но иногда, при изучении квадратного корня, учащиеся понимают это действие не совсем корректно, полагая, что 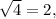 но одновременно с тем как бы и
но одновременно с тем как бы и 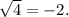 Это ошибка! Так понимать действие корня нельзя. Любой калькулятор покажет именно
Это ошибка! Так понимать действие корня нельзя. Любой калькулятор покажет именно 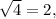 и это и есть верный результат вычислений, поскольку он единственный, так как любое арифметическое действие должно давать ОДНОЗНАЧНЫЙ результат.
и это и есть верный результат вычислений, поскольку он единственный, так как любое арифметическое действие должно давать ОДНОЗНАЧНЫЙ результат.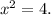 Корни этого нелинейного уравнения, как легко понять:
Корни этого нелинейного уравнения, как легко понять:  и
и 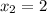 или в короткой записи
или в короткой записи 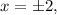 что равносильно
что равносильно 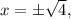 где сам «арифметический квадратный корень»
где сам «арифметический квадратный корень» 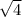 – это именно ПОЛОЖИТЕЛЬНОЕ число, а уж перед ним ставятся разные знаки, чтобы показать, что «корнями этого нелинейного уравнения» являются и само значение «квадратного арифметического корня» и число, противоположное ему. Аналогично, например, для уравнения:
– это именно ПОЛОЖИТЕЛЬНОЕ число, а уж перед ним ставятся разные знаки, чтобы показать, что «корнями этого нелинейного уравнения» являются и само значение «квадратного арифметического корня» и число, противоположное ему. Аналогично, например, для уравнения: 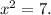 Корни этого нелинейного уравнения, как легко понять:
Корни этого нелинейного уравнения, как легко понять: 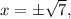 где сам «арифметический квадратный корень»
где сам «арифметический квадратный корень» 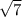 – это именно ПОЛОЖИТЕЛЬНОЕ число, а уж перед ним ставятся разные знаки, чтобы показать, что «корнями этого нелинейного уравнения» являются и само значение «квадратного арифметического корня» и число, противоположное ему.
– это именно ПОЛОЖИТЕЛЬНОЕ число, а уж перед ним ставятся разные знаки, чтобы показать, что «корнями этого нелинейного уравнения» являются и само значение «квадратного арифметического корня» и число, противоположное ему.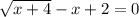 ;
;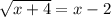 ;
;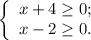
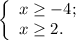
![x \in [ 2 ; +\infty ]](/tpl/images/0480/8307/22de1.png) ;
;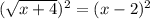 ;
;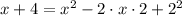 ;
;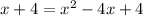 ;
;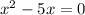 ;
;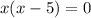 ;
;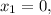 это не соответствует ОДЗ, поскольку
это не соответствует ОДЗ, поскольку ![x_1 = 0 \notin [ 2 ; +\infty ]](/tpl/images/0480/8307/72ba8.png) ;
;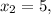 что соответствует ОДЗ, поскольку
что соответствует ОДЗ, поскольку ![x_2 = 5 \in [ 2 ; +\infty ]](/tpl/images/0480/8307/2f42f.png) ;
;