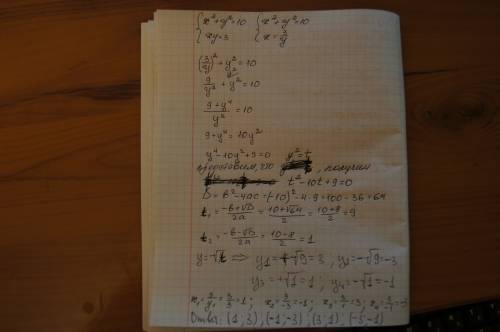
1) Дано: 3^(5x-2,5)≤√3, приводим к общему основанию: 3^(5x-2,5)≤3^0,5, т.к. основания одинаковые, работаем только с показателями степени и решаем неравенство: 5x-2,5≤0,5 ⇒ x≤3/5 или x≤0,6
2) Дано: (x²-1)*√(4x+7)≤0
а) Сначала выполняем ОДЗ для подкоренного выражения, которое никогда не бывает меньше нуля: 4x+7≥0 ⇒ x≥-7/4 или x≥-1,75
б) Так как всё неравенство меньше либо равно нулю, то это может быть лишь в том случае, когда x^2-1 либо меньше нуля, либо равно нулю. Зная, что произведение двух чисел равно нулю только когда оба множителя равны нулю, решим второе неравенство:
x²-1≤0, x²≤1 ⇒ x≤ 1 и x ≤ -1
в) Объедением наше решение (x≤ 1 и x ≤ -1) с ОДЗ (x≥-1,75) и получаем, что наш икс лежит в промежутке [-1,75;-1]
ответ: x∈[-1,75;-1]
3) Дано: log_2(x-2)+log_2(x)=0,5log_3(9).
Упростим его до вида: log_2(x-2)+log_2(x)=1 (в правой части получилась единица по свойству логарифмов, показатель 9 можно записать в виде 3² и степень переноситься в множитель логарифма, сокращаясь с 0,5 и в итоге получается log_3(3) либо просто один). Теперь приводим уравнение к общему основанию, логарифмируя единицу:
log_2(x-2)+log_2(x) = log_2(2), log_2(x²-2x) = log_2(2); т.к. в ообоих частях у нас получилось одинаковое основание логарифма 2, то работаем только с выражениями под логарифмом:
x²-2x=2, x²-2x-2=0, решаем как квадратное уравнение по дискриминанту: √D = √(4+8) = √12 = 2√3
Корни данного уравнения: x₁ = 2+√3 и x₂ = 2-√3
Объяснение:
|x -1| + |x +3| ≤ 4
Решим это неравенство методом интервалов.
Найдем нули подмодульных выражений:
х - 1 =0 → х = 1
х + 3 = 0 → х = - 3
Эти значения разбивают числовую ось на три интервала:
х ∈ (-∞; - 3] ; (-3; 1]; (1; + ∞)
Решим заданное неравенство на каждом из этих промежутков.
1) 1) x∈ (-∞; - 3], при этом неравенство примет вид:
- (х - 1) - (х + 3) ≤ 4
-х + 1 - х - 3 ≤ 4
-2х ≤ 6
х ≥ - 3
Пересекая найденное решение x∈ [- 3; +∞) c рассматриваемым интервалом x∈ (-∞; - 3] , получаем решение x = - 3
2) х ∈ (-3; 1]
- (х - 1) + х + 3 ≤ 4
0*х ≤ 4 → х - любое число. Учитывая интервал, х х ∈ (-3; 1]
3) х ∈ (1; + ∞)
х - 1 + х + 3 ≤ 4
2х ≤ 2
х ≤ 1 → х ∈ (- ∞; 1]
Для получения окончательного ответа объединим полученные решения:
x ∈ [- 3] ∪ (-3; 1] ∪ (- ∞; 1]
ответ: х ∈ [-3; 1]
(3/y)^2+y^2=109+y^4=10y^4=1y=+-1.1случай)у=1х=3.2 случай)у=-1х=-3ответ(3;1)и(-3;-1)