y = 4x - x² - Квадратичная функция, график - парабола, ветви направлены вниз ( a = -1). Максимальное значение принимает в вершине, минимальное значение не имеет, снизу не ограничена.
a) Координаты вершины параболы
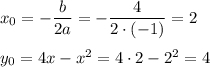
x₀=2 ∈ [0; 3] ⇒ x₀=2 - точка максимума функции попадает в заданный интервал, наибольшее значение функции y₀ = 4.
Значения функции на границах интервала
x = 0; y = 4·0 - 0² = 0
x = 3; y = 4·3 - 3² = 3
Наименьшее значение y = 0 при x = 0.
б) x∈(-∞; 2] - функция возрастает
x∈[2; +∞) - функция убывает
в) 4x - x² < 0 ⇔ x (4 - x) < 0
Метод интервалов : x₁ = 0; x₂ = 4
------------ (0) +++++++++ (4) -----------> x
x∈(-∞; 0) ∪ (4; +∞)
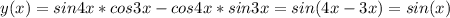
есть 
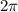
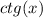равен 
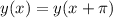
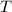- искомый период, тогда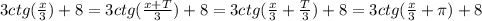
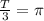
относительно оси OX на 8 единиц вверх, также не влияя на период
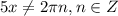
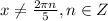
- это симметричное относительно начала координат множество точек,
также симметрична относительно начала координат. Это означает, что есть смысл проверять функцию на парность, дальше.
