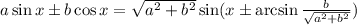
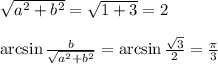
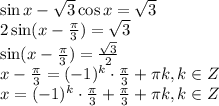
переносим минус три в левую часть, получаем
-2^x - 5х + 3 >= 0 делим на -1, при делении на отрицательное число знаки меняются
2^х + 5х - 3 <= 0 рашаем с дискрименанта
D = (-5)^2 - (-3)*2*4 = 25 + 24 = 49
x1 = -5 + √49 / (2*2) = (-5+7)/4 = 2/4 = 0.5
x2 = ( -5- √49) /( 2*2) = (-5-7)/4 = -12/4 = -3
2(x-0.5)(x+3)<=0
(2x-1)(x+3)<=0
ресуем прямую с точками -3 и 0.5 принадлежавшими ей
до - 3 ур-во приобретает положительное значение (не подходит)
от -3 до 0.5 отрицательно (подходит)
от 0.5 положительное (не подходит)
х принадлежит [-3; 0.5]
log(5x-4x^2) (4^-x) > 0
log(5x-4x^2) (4^-x) > log(5x-4x^2) 1
данное неравенство равносильно совокупности 2х систем:
1) 5x-4x^2 > 1
4^-x > 1
2) 0 < 5x-4x^2 < 1
4^-x < 1
1) а) 5x-4x^2 -1 > 0
4x^2 - 5x + 1 < 0
(x - 1)(x - 0,25) < 0
0,25 < x < 1
б) 4^-x > 1
4^-x > 4^0
-x > 0
x < 0
Т.е. 0,25 < x < 1 и х < 0
нет решений
2) а)
0 < 5x-4x^2 < 1
5x-4x^2 > 0
x(5 - 4x) > 0
0 < x < 5/4
5x-4x^2 < 1
5x-4x^2 - 1 < 0
2x^2 - 5x + 1 > 0
(x - 1)(x - 0,25) > 0
x < 0,25 x >1
б)
4^-x < 1
4^-x < 4^0
-х < 0
x > 0
Т.о. 0 < x < 5/4
x < 0,25 x >1
x > 0
Получим, (0; 0,25) и (1;1,25)