1. Уравнение можно решить так же, как это сделал(а) Agnesmile02464, но можно ещё сделать через дискриминант.
x^2 - 6x - 7 = 0
D = b^2 - 4ac;
D = -6^2 - 4 * 1 * (-7) = 36 + 28 = 64
x = (-b +-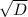 
)/2a
x1 = (6 +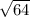 
)/2 * 1 = (6 + 8)/2 = 14/2 = 7
x2 = (6 - 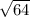)/2 * 1 = (6 - 8)/2 = -2/2 = -1
2. Для решения этого задания есть специальная формула, но я её благополучно забыл.) Попробую решить через систему. Для решения этого задания нам понадобится всеми любимая формула y=kx + b. Нужно взять две любые точки, через которые проходит прямая, и подставить. Получаем:
(-1;3) и (1;-3)
Подставляем в формулу, получаем систему:
{3 = -k + b
{-3 = k + b
Перенесем значения, чтобы были легче:
{k - b = -3
{-k - b = 3
Нам нужно найти k и b. Отнимем эти уравнения, чтобы избавиться от b и, для начала, найти k:
k - b - (-k) - (-b) = -3 - 3
k - b + k + b = -6
2k = -6
k = -3
Подставим в саааамое первое уравнение:
3 = - (-3) + b
3 = 3 + b
-b = 3 - 3
b = 0
k = -3, b = 0. Подставляем значения в y = kx + b и получаем функцию:
y = -3x
ответ 1)
Объяснение: Если что-то непонятно - не стесняйся и спрашивай ;)
В решении.
Объяснение:
Найдите значение выражений:
1) (3-x)²-x(x-21) = при x= -2,84
= 9 - 6х + х² - х² +21х =
= 9 + 15х =
=9 + 15 * (-2,84) =
=9 - 42,6 = -33,6.
2) d⁷×(d³)⁻¹ = при d= -2
= d⁷ * 1/d³ =
= d⁷/d³ = d⁷⁻³ = d⁴ = (-2)⁴ = 16.
3) a + (2y-a²)/a = при a= -10 и y=19
общий знаменатель а:
= (а*а + 2у - а²)/а =
= (а² + 2у - а²)/а =
=2у/а = 2*19/(-10) = 38/(-10) = -3,8.
Применяем формулу:
x² + 2xy + y² = (x + y)²
упростим левую часть:
(a + 4 + 6 - a)² = 10² = 100
100 = 100 доказано