Поскольку необходимо представить число 68 в виде суммы двух чисел, то пусть первое число х, тогда второе число (68-х). Тогда сумма квадратов слагаемых будет равна: х²+(68-х)²=х²+68²-2*68*х+х²=2х²-136х+4624
Здесь можно найти минимальное значение 2-мя 1) с производной (2х²-136х+4624)'=4x-136 4x-136=0 4x=136 x=136:4 х=34 Значит будет 2 одинаковых положительных числа 34 и 34.
2) с графика y=2х²-136х+4624 Это парабола - ветви направлены вверх. Значит наименьшее значение будет в вершине параболы. х₀=-b/2a=-(-136)/4=34
Задание: разложить на множители. множители - компоненты при умножении ⇒выражение представляет собой произведение многочленов. преобразовать данное выражение так, чтобы в каждом слагаемом были одинаковые множители. 1. m-n+p(m-n). 3-е слагаемое состоит из двух множителей р и (m-n), значит первое и второе слагаемое группируем и записываем (m-n). необходимо представить в виде произведения двух множителей. один множитель (m-n), второй множитель в этом слагаемом может быть только 1. получаем: m-n+p(m-n)=(m-n)*1+p*(m-n)=(m-n)*(1-p)
Дано: b₁=-1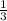 , bₙ₋₁=-3bₙ
, bₙ₋₁=-3bₙ
Значит, знаменатель прогрессии q = -3. Тогда:
b₇=b₁*q⁶=-1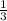 *(-3)⁶=-972
*(-3)⁶=-972