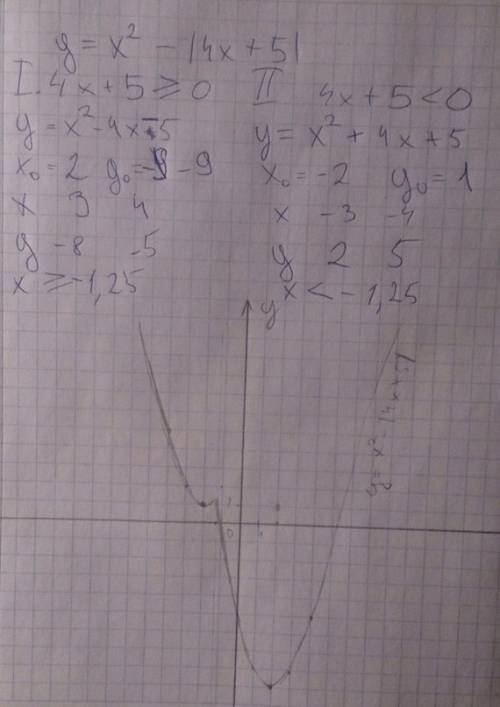
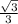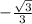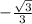;
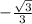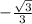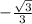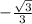; и;););)+2kπ, k∈Z;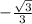)+2kπ, k∈Z;
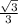)+2kπ, k∈Z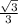)+π-2kπ, k∈Z;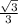)+2kπ, k∈Z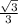)+π+2kπ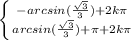, k∈Z;
, k∈Z
Объяснение:
Квадраты кончаются на такие цифры:
1^2=1; 2^2=4; 3^2=9; 4^2=16; 5^2=25; 6^2=36; 7^2=49; 8^2=64; 9^2=81; 10^2=100
У нас три последовательных числа.
Если первое кончается на 1, то сумма квадратов кончается на
1+4+9=14, то есть на 4, как второе число.
Чтобы сумма квадратов была нечетной, первое число должно быть четным.
Если первое кончается на 2, то сумма кончается на 4+9+16=29, то есть на 9.
Если первое кончается на 4, то сумма кончается на 16+25+36=77, то есть на 7.
Если первое кончается на 6, то сумма кончается на 36+49+64=149, то есть на 9.
Если первое кончается на 8, то сумма кончается на 64+81+100=245, то есть на 5.
Если первое кончается на 0, то сумма кончается на 0+1+4=5.
Ни при каких условиях сумма трех квадратов последовательных чисел не может кончаться на 3.
ответ: правильное второе число.
