По формулам приведения:
если в тригонометрической формуле встречается выражение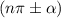 , где
, где 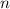 — целое число, то вид тригонометрической функции не меняется; знак тригонометрической функции может меняться в зависимости, в какой четверти находилась данная функция. Например,
— целое число, то вид тригонометрической функции не меняется; знак тригонометрической функции может меняться в зависимости, в какой четверти находилась данная функция. Например, 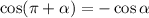 (минус, потому что общий угол будет находиться в третьей четверти).если в тригонометрической формуле встречается выражение
(минус, потому что общий угол будет находиться в третьей четверти).если в тригонометрической формуле встречается выражение 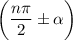 , где
, где 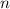 — целое число, то вид тригонометрической функции меняется; знак тригонометрической функции может меняться в зависимости, в какой четверти находилась данная функция. Например,
— целое число, то вид тригонометрической функции меняется; знак тригонометрической функции может меняться в зависимости, в какой четверти находилась данная функция. Например, 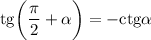 (минус, потому что общий угол будет находиться во второй четверти).
(минус, потому что общий угол будет находиться во второй четверти).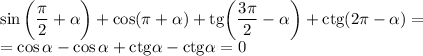
4/t+t^2=15, откуда t^3-15t+4=0.
Поскольку решаем школьными методами, то можно поискать целый корень, который делит младший коэффициент, т.е. является делителем числа 4. Это могут быть -1, 1, -2, 2, -4, 4. Подходит t=-4. Значит, переписываем уравнение в виде
t^3-15t+4=(t^3+4t^2)-(4t^2+16t)+(t+4)=(t+4)(t^2-4t+1)=0
Решаем t^2-4t+1=0, получаем
x=-4-2=-6 и
Т.е., ответ: -6 и