В решении.
Объяснение:
7) (а⁻⁴)⁸ = а⁻³²;
8) (а³)⁻⁷ * (а⁻⁴)⁻⁵ : (а⁻⁵)⁸ =
= а⁻²¹ * а²⁰ : а⁻⁴⁰ =
= а⁻¹ : а⁻⁴⁰ = 1/а : 1/а⁴⁰ = (1*а⁴⁰)/(а*1) = а³⁹;
9) (а⁵b⁻³c⁴)⁻¹⁰ =
= a⁻⁵⁰b³⁰c⁻⁴⁰ = b³⁰/a⁵⁰c⁴⁰;
10) (a²b⁻³)⁻³ * (a⁻⁴b⁻⁹)⁶ =
= a⁻⁶b⁹ * a⁻²⁴b⁻⁵⁴ =
= b⁹/a⁶ * 1/a²⁴b⁵⁴ =
=(b⁹ * 1)/(a⁶*a²⁴b⁵⁴) =
= 1/a⁶⁺²⁴b⁵⁴⁻⁹ =
= 1/a³⁰b⁴⁵;
11) ((a¹²b⁻⁴)/(c⁵d⁻¹³))⁻² =
=(a⁻²⁴b⁸)/(c⁻¹⁰d²⁶) =
=b⁸/a²⁴ : d²⁶/c¹⁰ =
= (b⁸c¹⁰)/(a²⁴d²⁶);
12) (a⁷/b⁻³)⁻⁴ * (a⁻³/b⁹)⁻¹² =
= (a⁻²⁸/b¹²) * (a³⁶/b⁻¹⁰⁸) =
= (1/a²⁸ : b¹²) * (a³⁶ : 1/b¹⁰⁸) =
= 1/(a²⁸b¹²) * (a³⁶b¹⁰⁸) =
= (a³⁶b¹⁰⁸)/(a²⁸b¹²) =
= a⁸b⁹⁶.
Вычислить значение выражения:
4) 3⁻¹⁴ * 3⁻¹⁹ : 3⁻³⁴ =
= 3⁻³³ : 3⁻³⁴ =
= 1/3³³ : 1/3³⁴ =
=3³⁴/3³³ = 3;
5) (13⁻⁹)⁴ * (13⁻²)⁻¹⁸ =
= 13⁻³⁶ * 13³⁶ =
= 13³⁶/13³⁶ = 1;
6) (2⁻⁴ * (2⁻³)⁵)/((2⁻⁸)² * 2⁻³) =
= (2⁻⁴ * 2⁻¹⁵)/(2⁻¹⁶ * 2⁻³) =
=2⁻¹⁹/2⁻¹⁹ = 1.
Объяснение:
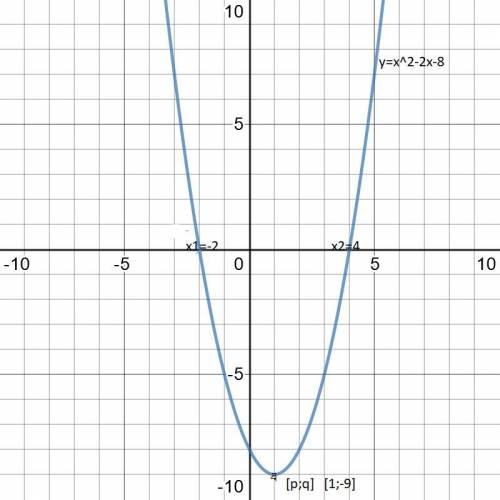
y=x²-2x-8
*ODZ : (-∞;∞)
*Набор значений: <-9;oo)
*Коэффициент a > 0 , Таким образом, функция убывает в интервале (-oo; 1> и увеличивается в интервале <1; oo)
*экстремумы: минимум для f (1)
*место пересечения функции с осью OY [0; -8]
f(0)=1*0^2-2*0-8
f(0)=-8
*вершина параболы (экстремум): [p; q]
p=-b/2a , q=-D/4a
p=- -2/2*1=2/2=1
q=-36/4*1=-36/4=-9
*нулевая позиция функции
X²-2x-8=0
Δ=(b²-4ac)=4+32=36
√Δ=6
x1=(2-6)/2=-4/2=-2
x2=(2+6)/2=8/2=4
x ∈ {-2;4}
( w załączeniu grafik funkcji kwadratowej)
х²+у²-16=2ху
х²+у²-4=-2ху
Отнимем из первого уравнения второе уравнение:
х²+у²-16-х²-у²+4=2ху+2ху
-12=4ху
ху=-12/4
ху=-3
х=-3/у
Подставим найденное значение х в любое из уравнений, например в первое:
(-3/у)²+у²-16=2*(-3/у)*у
9/у²+у²-16=-6
9/у²+у²-16+6=0
9/у²+у²-10=0 Приведём полученное уравнение к общему знаменателю у²:
9+у^4-10у^2=0
Обозначим у² переменной t, то есть у²=t, получим уравнение :
t²-10t+9=0
t1,2=5+-√(25-9)=5+-√16=5+-4
t1=5+4=9
t2=5-4=1
Подставим найденные значения t в у²=t
у²=9
у1,2=+-√9=+-3
у1=3
у2=-3
у²=+-1=+-√1=+-1
у3=1
у4=-1
Значения (у) найдены, найдём значения (х):
х=-3/у
х1=-3/3=-1
х2=-3/-3=1
х3=-3/1=-3
х4=-3/-1=3
ответ: х1=-1; х2=1; х3=-3; х4=3; у1=3; у2=-3; у3=1; у4=-1