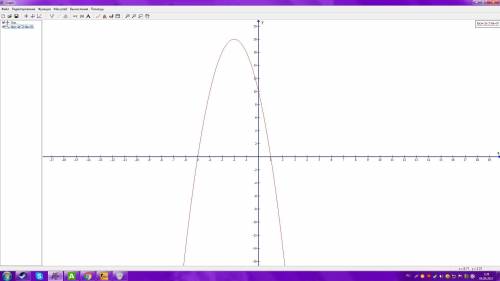
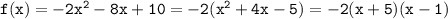; (график во вложении, если не понял)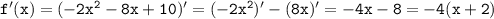
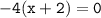, следовательно, производная имеет единственную критическую точку 
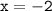; интервалы нам дают следующее: производная отрицательна на промежутке 
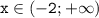, следовательно, функция на этом промежутке убивает, и наоборот, – возрастает функция на промежутке 
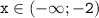, потому что производная на данном промежутке положительна.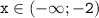 
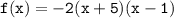должна быть положительна, следовательно, неравенство мы получаем следующее: 
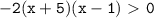; решение неравенства: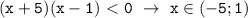 
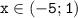
x^3+x^2+x+1=0
Групируем и выносим за скобки x^2
x^2*(x+1) + (x+1)=0
Выносим (x+1) за скобки:
(x+1)(x^2+1)=0
Для того чтобы уравнение было равно нулю один из множетелей долженбыть равен нулю.
x^2+1 =0 -- эта скобка не имеет коней.
x^2+1-- всегда болье нуля поскольку это парабола поднятая над ось x на 1 соотве
x+1 = 0 -- имеет корень x = -1
Решение задачи x = -1
надеюсь это)