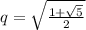
 - k-ый ((n-k)+1)-ый
- k-ый ((n-k)+1)-ый  - (k+1)-ый (n-k)ый
- (k+1)-ый (n-k)ый - n-ый обратный счет вверх 1-ый
- n-ый обратный счет вверх 1-ый 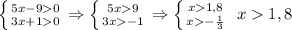
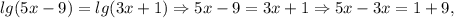
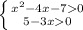
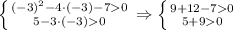
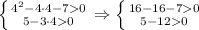
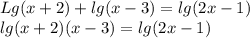 заменили сумму логарифмов логарифмом произведения.
заменили сумму логарифмов логарифмом произведения.
15х²+3у²=61х
умножим первое уравнение на(-3)
-15х²-3у²=-183,
15х²+3у²=61х
сложим первое уравнение со вторым, получим:
-183+61х=0,
61х=183,
х=183:61,
х=3
значение х=3 , подставим в уравнение: 5х²+у²=61,
5*9+у²=61,
45+у²=61,
у²=61-45,
у²=16,
у=-4,у=4
ответ:(3;-4),(3;4)