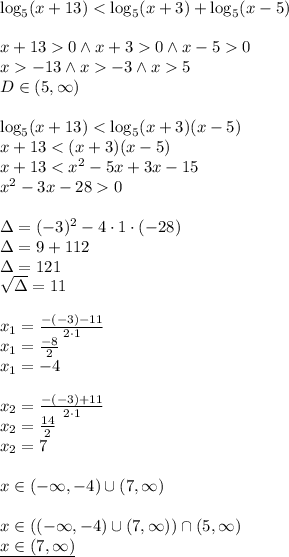
---------------------------------------------------------------------------
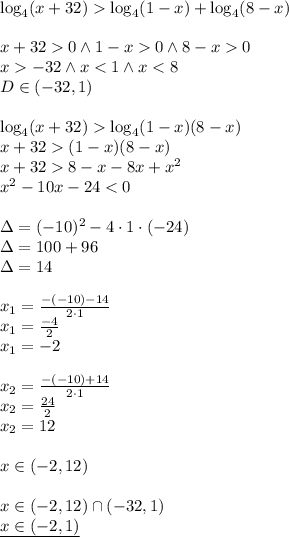
2222 - 111 - 99 + 5 = 2017.
Посмотрим, чему может равняться число . Так как выражение "- EEE - AA + R" больше или равно - 1086 (= - 999 - 88 + 1), то должно быть довольно близко к 2017. 3333 и 1111 не подходят, значит = 2222.
Теперь обратим внимание на число EEE. Пусть оно равно 222 или больше. Тогда у нас получится 2222 - 222 = 2000 или меньше. Теперь от этого числа нужно отнять некоторое двузначное и прибавить однозначное, то есть еще уменьшить число. Но так невозможно будет получить 2017. Значит, EEE = 111.
Мы имеем: 2222 - 111 = 2111. Если мы отнимем 94, то получим ровно 2017, но тогда R = 0 (ненатуральное). Тогда мы можем подставить A = 95, 96, 97, 98, 99 и получим соответственно R = 1, 2, 3, 4, 5. Но А должно состоять из одной цифры, так что A = 99, R = 5.
Примечание:
При решении ребуса мы учитывали то, что все числа являются натуральными, и не повторяются (то есть Y не может быть равно R и т. д.).
1) log{5} (x+13)<log{5} (x+3)+log{5}(x-5)
log{5} (x+13)<log{5}(x+3)(x-5)
ОДЗ: x+13>0 =>x>-13
x+3>0 => x>-3
x-5>0 => x>5
то есть x>5
x+13<(x+3)(x-5)
x+3<x^2-5x+3x-15
x^2-3x-28>0
Находим критические точки
D=121
x1=-4
x2=7
Методом интервалов определяем
-4>x>7
и с учетом OДЗ x>7
2) log{4}(x+32)>log{4}(1-x)+log{4}(8-x)
log{4}(x+32)>log{4}(1-x)(8-x)
x+32>(1-x)(8-x)
x+32>8-x-8x+x^2
x^2-10x-24<0
Находим критические точки
D=196
x1=-2
x2=12
Методом интервалов определяем
-2 <x<12