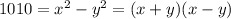
1010 - чётное число, чтобы разность была чётная, то оба квадрата должны одновременно быть либо чётными, либо нечётными, т.е. эти натуральные числа или оба чётные, или оба нечётные.
Разложим 1010 на простые множители: 1010=2*5*101
Число 1010 можно представить в виде произведения двух сомножителей:
1010=1010*1
1010=505*2
1010=202*5
1010=101*10
В любом случае получается, что один из сомножителей чётный, а другой нечётный. В случае же если оба числа чётные или оба нечётные, то сумма и разность этих двух чисел могут быть только чётными числами. Поэтому число 1010 нельзя представить в виде разности квадратов двух натуральных чисел.
ответ: НЕТ.
Пусть функция 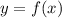 определена на отрезке
определена на отрезке ![[a;b]](/tpl/images/1361/6254/a6d4a.png)
Разобьём отрезок произвольным образом на n частей точками:
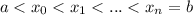
В каждом интервале произвольным образом выбираем точку
![c_{i}\in [x_{i-1};x_{i}]](/tpl/images/1361/6254/a2b9c.png)
Cумма
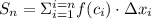 ,
,
где 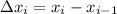 - длина частичного отрезка
- длина частичного отрезка ![[x_{i-1};x_{i}]](/tpl/images/1361/6254/3b10f.png) ,
,
называется интегральной суммой функции 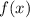 на отрезке
на отрезке ![[a;b]](/tpl/images/1361/6254/a6d4a.png) .
.
Определенным интегралом от функции 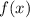 на отрезке
на отрезке ![[a;b]](/tpl/images/1361/6254/a6d4a.png) называется предел интегральных сумм
называется предел интегральных сумм 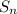 , при условии, что длина наибольшего частичного отрезка стремится к нулю
, при условии, что длина наибольшего частичного отрезка стремится к нулю
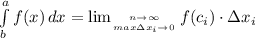
Геометрическая интерпретация определённого интеграла - площадь криволинейной трапеции
основания = 3
3log(x + 2) = 3
осн-е =3
log( x + 2) = 1
осн-е = 3
x + 2 = 3
x = 1
Теперь надо учесть ОДЗ х + 2 > 0 ⇒ x > -2
ответ: х = 1