прощения, но решение получилось слишком сложным :(
q - знаменатель геом. прогр.
d - сумма арифм. прогрессии
a - первый член ар. прогр.
b - первый член геом. прогр.
1) a+d+a+2d=2a+3d=12; также b+bq=b(1+q)=12; также bq+a+d=12
2) a+2d=bq
3) a+d=b
4) a+bq^2=14
из b(1+q)=12:
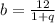
из a+2d=bq и a+d=b выражаем b+d=bq -> d=bq-b=b(q-1)
т.е. 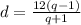
из a+bq^2=14 выразим a=14
Подставим в 2a+3d=12 получим квадратное уравнение вида:

После всех приведений и сокращений и с учетом, что занменатель д.б. не равен 0, получим:
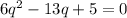
Решая єто уравнения получим, что q=5/3 - не подходит, т.к. в условии числа д.б. целыми и q=1/2.
Отсюда b=8, a=12, d=-4
Получаем последовательность:
12 8 4 2
Решение: Пусть a,b,c,d – данные последовательно записанные числа. Тогда по условию
a+d=22 (1)
b+c=20 (2)
Из свойств арифметической и геометрической прогрессии имеем:
a+c=2*b (3)
c^2=b*d (4)
Из (2) получим b=20-c (5).
Сложив (1) и (2), получим a+b+c+d=22+20=42, использовав (3) и (5), получим
3*b+d=42, d=42-3*b=42-3*(20-c)=42-60+3*c=3*c-18, то есть
d=3*c-18 (6).
Использовав (4), (5), (6), получим
c^2=(20-c)*(3c-18). Решаем:
c^2=60*c-360-3*c^2+18*c=-3c^2+78c-360.
4*c^2-78*c+360=0
2*c^2-39*c+180=0.
d=39^2-4*2*180=81
c1=(39-9)\(2*2)=30\4=15\2=7.5
c2=(39+9)\(2*2)=12
Из (1), (6) получим
а=22-d=22-(3*c-18)=40-3*c (7).
Используя (5), (6), (7), получим
a1=40-3*7.5=17.5
a2=40-3*12=4
b1=20-7.5=12.5
b2=20-12=8
d1=3*7.5-18=4.5
d2=3*12-18=18
Таким образом получили две последовательности 17.5;12.5;7.5;4.5 и
4;8;12;18
ответ: 17.5;12.5;7.5;4.5 или 4;8;12;18
Пусть x и y-натуральные числа.
При четном n очевидно что:
(+-x)^n-(+-y)^n=91
x^n-y^n=91
При нечетном n:
1) x^n-y^n=91
2) (-x)^n-y^n=91
-x^n-y^n<0 (искомый случай невозможен)
3) x^n-(-y)^n=x^n+y^n=91
4) (-x)^n-(-y)^n=y^n-x^n=91 (По своему характеру аналогичен случаю 1) )
Итак у нас в общем итоге два случая:
1) x^n-y^n=91
2) x^n+y^n=91
где x,y-натуральные числа.
Рассмотрим 1 случай:
Очевидно что x>y:
Тогда по формуле разности степеней получим:
x^n-y^n=(x-y)*(x^n-1+x^n-2*y+y^n-2*x+y^n-1)=91
Правая скобка является делителем числа 91. То есть она может быть равна: {1,7,13,91}
тк x≠y то тк n>3 и x,y-натуральные числа
то очевидно :
x^n-1+x^n-2*y+y^n-2*x+y^n-1>=x^3+x^2*y+x*y^2+y^3>=2^3+2^2*1+2*1+1=
=15>13
А значит: x^n-1+x^n-2*y+y^n-2*x+y^n-1=91
x-y=1
Положим что y>2 тогда:
x^n-1+x^n-2*y+y^n-2*x+y^n-1>=x^3+x^2*y+x*y^2+y^3>=
>=3^3+3^2*4+3*4^2+4^3=175>91
Значит y=1 или 2
при y=1 x=2
2^n-1=91
2^n=92 (неверно)
при y=2 x=3
3^n-2^n=91
при n=4 не выполняется.
Тогда n>4
3^n-2^n>=3^5-2^5=211>91.
(То есть такой случай невозможен)
2) Осталось рассмотреть случай:
x^n+y^n=91
Положив что x,y>1
x^n+y^n>=2^4+3^4=97>91
То есть x=1 или y значения не имеет:
x^n=90 (Невозможно)
Значит 91 в виде разности степеней не раскладывается.