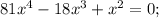
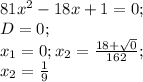
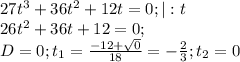
Предположим, что утверждения a) и в) верны. Обозначим задуманное число через x. Согласно двум утверждениям Пети x + 51 = n^2 и x - 38 = k^2, где n и k - натуральные. Тогда n^2 - k^2 = (n-k)*(n+k) = x + 51 - x + 38 = 51 + 38 =89. Поскольку 89 простое число, то единственным вариантом будет n - k = 1, а n + k = 89. Тогда из первого равенства n = k + 1 и из второго n + k = k + 1 + k = 2k + 1 = 89 => k = 88/2 = 44. Тогда n = k + 1 = 45. Следовательно n^2 = 45^2 = 2025, а k^2 = 44^2 = 1936. Искомое число x = 2025-51 = 1936 + 38 = 1974. Видим, что оно оканчивается на 4. Следовательно утверждение о том, что оно оканчивается на 1 неверно.
ответ: 1974.
x²((9x)² -2*(9x)*1 +1) =0;
x²(9x -1)² = 0 ;
[ x =0; 9x -1 =0. [ x=0; x=1/9.
ответ: 0 ; 1/9.
27t³ +36t² +12t =0 ;
3t(9t² +12t +4) =0;
3t(3t +2)² =0;
[ t =0; 3t +2 =0. [ t=0 ;t = - 2/3.
ответ: 0 ; - 2/3.