Задание 1.
1) 15ab+10bc= 5b(3a+2c).
2)3x²+6xy+3y²= 3(x²+2xy+y²)= 3(x+y)².
3)6x(x-1)-(1-x)= 6x(x-1)+(x-1)= (x-1)(6x+1).
4)3a³+3= 3(a³+1)= 3(a+1)(a²-a+1).
5) 2a-2b+a²-b²= 2(a-b)+(a-b)(a+b)= (a-b)(2+a+b).
6)-3x(x+3)+x³+27= -3x(x+3)+(x+3)(x²-3х+9)= (х+3)(-3х+х²-3х+9)= (х+3)(х²-6х+9)=(х+3)(х-3)².
Задание 2.
(43²-17²):(43²-2•43•17+17²)= ((43-17)(43+17)) ÷ (43-17)²= 26•60÷26²= 60÷26=30/13= 2 4/13 (две целых четыре тринадцатых).
P.S. Возможно Вы неправильно списали с условия во втором задании, пересмотрите условие, я заменила "+" на знак умножения.
, ч — время движения мотоциклиста до места встречи, тогда 
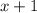, ч — время велосипедиста.
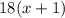, км — расстояние, преодоленное велосипедистом;
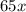, км — расстояние, преодоленное мотоциклистом (искомое).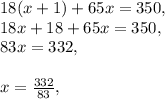
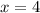часа двигался мотоциклист до места встречи;
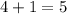часов был в пути велосипедист.
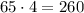км.
1:8=1/8 часть - заказа выполняет ученик за 1 час.
1:6=1/6 часть - заказа выполняет мастер за 1 час.
1/8 + 1/6 = 3/24 + 4/24 = 7/24 заказа - выполняют мастер и ученик за 1 час вместе.
7 : 7/24 = 7 * 24/7 = 24 детали - составляет заказ.
ответ: 24 детали.
6. 2*16=32 человека - удалось бы расселить, если бы все 16 номеров были двухместными.
42-32=10 человек - остались бы лишними, если бы все 16 номеров были двухместными. Это же и есть количество трехместных номеров, поскольку эти 10 человек будут по одному "доселены" в наши предполагаемо двухместные номера (по 2 там уже есть - см.1 действие).
16-10=6 номеров - двухместных было.
Проверим: 10*3+6*2=30+12=42 человека - верно.