x^4-8x^2-9=0
делаем замену х^2=t, t больше или равно нулю
t^2-8t-9=0
t1+t2=8
t1*t2=-9
t1=9 t2=-1
Возвратная замена:
x^2=9
x=-3;3
1.
А множество натуральных
Б кольцо целых
В множество натуральных
Г поле рациональных
2.
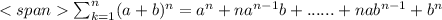
Каждое слагаемое в скобках содержится в правой части тождества в степени ниже чем 1 ровно 1 раз.
То есть все слагаемые,кроме последних после раскрытия исходных скобок будут кратны 10 и заканчиваться на 0.произведение 
будет определять цифру,на которую оканчивается произведение исходных чисел.
Число 6 в любой натуральной степени оканчивается на 6,1 в любой степени даст 1.Произведение равно 6.
Это и есть цифра на которую оканчивается исходное произведение.
1 вариант решения.
|x-4|=8
Решим уравнение x-4=0
x=4
Отметим точу на координатной прямой
4>x
Получилось 2 промежутка (-бесонечности до 4) (4 до + бесконечности)
1) Берем любое число из 1 промежутка, например 5, модуль раскрываеться положительно
x-4=8
x=12
2) Берем любое число из 2 промежутка, например 3, модуль раскрываеться отрицательно
-x+4=8
x=-4
ответ: x=12 ; x=-4 .
Как решаються уравнения подобного типа?
1) Приравниваем все уравнения стоящие в модуле к нулю
2) Решаем их, и находим точки
3) Отмечаем точки на числовой прямой
4) Из каждого промежутка берем по любому число(лучше не все сразу, а по порядку)
5) Решаем главное решение, с учетом того, как расрылся модуль(Если число получившееся больше 0, то модуль расрываеться положительно, если меньше 0, то наоборот)
ответом и будут получившеяся числа. Так можно решить хоть уравнение с 100 модулей, главное не ошибиться при расчетах
2 вариант решения.
|x-4|=8
Возведем все в квадрат(Зачем? Если мы это сделаем, то выражение в модуле сразу станет положительным, и модуль убереться)
(x-4)^2=64
x^2-8x+16-64=0
x^2-8x-48=0
D=64+4*48*1=64+192=256
x1=8+16/2=12;
x2=8-16/2=-4;
ответ: x=12; x=-4
x^4-8x^2-9=0,
x^2=a,
a^2-8a-9=0,
По теореме Виета,
a1=-1<0, a2=9,
x^2=9,
x1=-3,
x2=3.