а) а∈[0; +оо).
б) а∈(-оо; 0]
в) х∈R.
г) х∈(-оо; 0]
д) х∈[6; +оо).
Объяснение:
а) √а , а≥0, а∈[0; +оо).
б) √-а, а≤0, а∈(-оо; 0]
в) √x^2 = lxl, x - любое действительное число, х∈R.
г) √- 361x, -361x ≥0, тогда х≤0, х∈(-оо; 0]
д) √(x -6), х-6≥0, х≥6, х∈[6; +оо).
(x^3+4x^2-9x-36)/(x^3+2x^2-11x-12)
Разложим числитель на множители:
x^3+4x^2-9x-36= (x^3+4x^2)-(9x+36)=x^2(x+4)-9(x+4)=(x^2-9)(x+4)=(x-3)(x+3)(x+4)
Разложим знаменатель на множители:
x^3+2x^2-11x-12
Попробуем подобрать число, при подстановке которого наше выражение равно нулю. Первое такое число "-1". Разделим наш знаменатель на х+1:
x^3+2x^2-11x-12 | x+1
x^3 +x^2 x^2+x-12
x^2 -11x
x^2 + x
-12x-12
-12x-12
0
Мы получили квадратное уравнение х^2+x-12,
корнями которого будут числа "3" и "-4".
Итак, x^3+2x^2-11x-12=(х+1)(х-3)(х+4)
Наша дробь примет вид (x-3)(x+3)(x+4)/(х+1)(х-3)(х+4)=(х+3)/(х+1)
Пусть 1 - это длина всего пути
х км/ч - скорость первого автомобиля (ОДЗ: x>0)
1/х час - время, затраченное на весь путь первым автомобилем
1/2 : 30 = 1/60 час - время, затраченное на первую половину пути вторым автомобилем
1/2 : (х+9) = 1/(2х+18) час - время, затраченное на вторую половину пути вторым автомобилем
По условию время, затраченное на весь путь первым автомобилем равно времени, затраченному на весь путь вторым автомобилем, получаем уравнение:
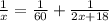
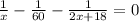
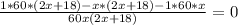
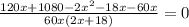
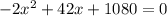
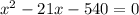
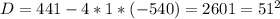
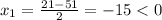
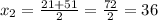 км/ч - скорость первого автомобиля
км/ч - скорость первого автомобиля
ответ: 36 км/ч
ответ: а) при положительных а или при а=0 (подкоренное выражение под квадратным корнем должно быть положительно или нуль);
б) при отрицательных а или при а=0, по той же причине;
в) при любых х, так как любое число в квадрате больше или равно нулю;
г) при отрицательных х или при х=0, объяснение как и в а);
д) при х ≥6, объяснение как и для а).
Объяснение: