ответ: первый случай, A=60°, C=30°
Второй случай, C=60°,A=30°
Объяснение:
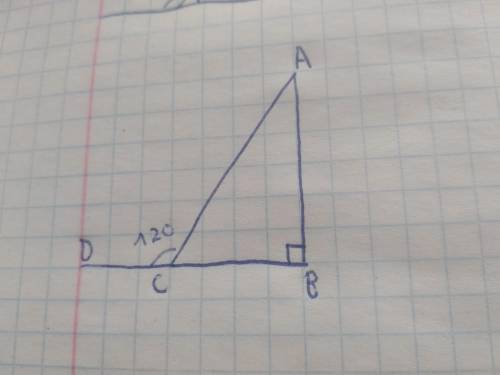
Для начала нарисуем прямоугольный треугольник ABC. Позже нарисуем внешний угол к углу C,обозначим этот внешний угол, как ACD. По условию ACD=120, а так как внешние углы-это углы, смежные с каким-нибудь углом треугольника, то ACD+C=180 C=180-120=60°. Из теоремы суммы углов треугольника, угол A=180-60-90=30°.
Рассмотрим 2 случай:
Нарисуем снова прямоугольный треугольник ABC и нарисуем внешний угол к углу a, обозначим его, как BAD. По условию угол BAD=120°,а так как внешний угол- это угол, смежный с каким-нибудь углом в треугольнике, то угол A=60°,из теоремы суммы углов, угол C=180-90-60=30
1. х² + 4х - 5 = 0
a=1 b=4 c=-5
x0= -b/2a= -4/2×1= -4/2= -2
y0= y(x0) = (-2)²+4×(-2)-5 = -9
ответ: -2 и -9
2. x² - 8x - 9 = 0
a=1 b=-8 c=-9
x0= -b/2a = 8/2×1 = 4/2 = 2
y0= y(x0) = 2²-8×2-9 = -21
ответ: 2 и 21
3. x² + x - 6 = 0
a= 1 b=1 c=-6
x0= -b/2a = -1/2×1 = -1/2= -0,5
y0= y(x0) = -0,5²+0,5-6 = -5,75
ответ: -0,5 и -5,75
4. х² - 6x - 7 = 0
a= 1 b=-6 c=-7
x0= -b/2a= -6/2×1= -6/2= -3
y0= y(x0) = -3²-6×(-3)-7= 2
ответ: -3 и 2
5. x² + 6x - 40 = 0
a=1 b= 6 c=-40
x0= -b/2a= -6/2×1= -6/2= -3
y0= y(x0) = -3²+6×(-3)-40 = -67
ответ: -3 и -67
6. x² - x - 2 = 0
a=1 b=-1 c=-2
x0= -b/2a= 1/2×1 = 1/2 = 0,5
y0= y(x0) = 0,5²-0,5-2 = -2,25
ответ: 0,5 и -2,25
Удачи!
1) Он всегда проходит через точку (0;1)
2) Он никогда не пересекает ось oX, а лишь подбирается к ней всё ближе и ближе при меньшем x.
Таким образом, строите график y = 2^x, подставляя целые x (рис.1)
Опускаете всё это дело на 2 единицы вниз (рис 2)
Теперь решим график функции:
1) D(x) = (-∞; +∞) E(y) = (-2;+∞)
2) x = 0 при y = -1; y = 0 при x = 1
3) Функция отрицательна на промежутке (-∞;0);
Функция положительна на промежутке (0;+∞);
4) Функция возрастает на промежутке (-∞;+∞)
5) Функция общего вида, так как f(x) ≠ f(-x) и f(x) ≠ -f(x)
6) Функция ограничена снизу прямой y = -2
7) Функция непериодическая
8) Точек минимума и максимума нет
9) Минимальных и максимальных значений нет
10) Функция выпукла вниз